※サンプル・コード掲載
1.あらすじ
ビタビアルゴリズム、おそらく人工知能について興味を持っている方で、音声認識、音声合成関連の仕事や、勉強をされている方には馴染みの言葉かと思います。
特に、音声認識分野での活用が多く、ビタビアルゴリズムを活用して、入力された音声信号から、最もそれらしい文字列を見つけ出す際に使用されます。
ビタビアルゴリズムとは何かを簡単に説明すると、何かの状態が与えられた時に、現在の状態に基づいて、その後に生じる状態の最も尤らしい(最も起こり得る)並びを探索するアルゴリズムで、動的計画法の一種であり、特に隠れマルコフモデルに基づいています。
それでは、以下詳しく見ていきましょう。
2.動的計画法とは?
動的計画法とは何か?なにやら難しそうな言葉で、あまり聞き馴染みの無い言葉かもしれませんが、今回の主題であるビタビアルゴリズムや、人工知能を支える技術の一つである機械学習の中で用いられている等、その活用の場面は幅広くなっています。
動的計画法を簡単に説明すると、対象の問題を、複数の部分問題に分解して、部分問題の計算を記録しながら解いていく手法です。
これをもう少し噛み砕くと、下記2つの要素から構成されています。
- 分割統治法: 部分問題を解いて、その結果を用いて、全体の問題を解く方法
- メモ化: 部分問題の計算結果を再利用する方法
つまり、このように全体としては大きな問題を、小さく分解して、それに対する解をうまく使い回し、結果として大きな問題を解く最適化の方法となります。
ここでは、アルゴリズムレベルで、動的計画法について説明する事はしませんが、プログラミングで動的計画法を行うためには、一般的には、for文や、再帰文等の繰り返しのプログラムの中で、計算結果を配列に保存する等の方法でメモ化を行い、それを、繰り返しの処理の中で効率的に活用していき、結果を積み上げ(ボトムアップ)ていく方法です。
これにより、プログラマの間では有名な、フィナボッチ数列問題や、ハノイの塔問題等を効率よく解いていくことが可能になります。
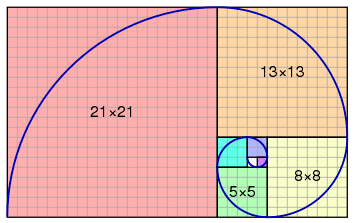
引用: https://en.wikipedia.org/wiki/Fibonacci_number
既に説明している通り、ビタビアルゴリズムも動的計画法の一種であり、こちらで説明したような、分割と、メモ化のアプローチを使って、最尤の並びを探索していくわけです。
3.ビタビアルゴリズムの詳細解説
それでは、本題であるビタビアルゴリズムそのものについて、その方法の詳細を小項目を設けて、なるべく詳しく解説していきます。
3-1.有限オートマトン
有限オートマトンとは有限状態機械とも言われますが、それは何かというと、デジタル回路の設計や、プログラムの設計等によく用いられますが、ある、有限の状態(リストアップ可能な状態)を定義して、そして、その状態から、次の状態へ遷移する際の組み合わせから構成される数学的に抽象化された「ふるまいモデル」の事です。
これだけ聞いてもよくわからないかと思いますが、プログラマであれば二分木のデータ構造について、プログラミングする機会はあったかと思います。
二分木を探索する際には、あるノードから、次のノードに移動する際に、何かしらの条件で、挙動を振り分けて、この条件に基づいて、次のノードを決定するかと思います。
そして、現在いるノードがまさに、現在の状態を表しており、次のノードに移る事が遷移となります。
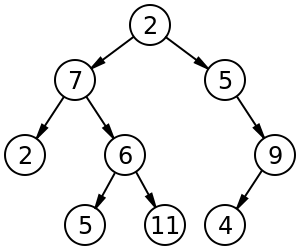
引用: https://en.wikipedia.org/wiki/Binary_tree
ふわっとでも良いので、有限オートマトンのイメージを理解して頂けると、以降の説明が理解しやすいかと思います。
決定木に関しては、決定木の2つの種類とランダムフォレストによる機械学習入門 をご参照下さい。
3-2.マルコフ連鎖
マルコフ連鎖とは、未来の状態は現在の状態にのみによって決定され、過去の状態に依存しないという確率過程の、マルコフ過程のうちの、とりうる状態が、有限または、加算で表現されるものを指しています。
特に、時間が離散のものを指している場合が多い様です。
マルコフ連鎖は、現在の状態が決定されていれば、過去、または未来は独立なものとみなし、それを数式的に表現すると以下のようになります。
![]()
一見、複雑にも見えますが、数式中のXnは、それぞれの状態を表しており、状態空間と呼ばれ、簡単に要約すると、次の状態(Xn+1)は、今の状態(Xn)によって決定されるという事を表しています。
3-3.隠れマルコフモデル
隠れマルコフモデル、この言葉も音声認識等をされている方には馴染みの深い言葉かと思いますが、この隠れマルコフモデルとは、マルコフ過程の一種で、観測されない(隠れた)状態をもつものとなります。
また、これが隠れマルコフモデルの名前の由来です。
おそらく、この名前をお聞きになり、何が隠れているのかと疑問になった読者の方は多いかと思いますが、これで、その謎が解けたかと思います。
先に説明したマルコフ連鎖では状態は直接観測されるので、状態の確率遷移がパラメータとなります。
正確にいうと、隠れマルコフモデルのパラメータは、遷移確率と、出力確率の2つとなります。
対して、隠れマルコフモデルでは状態は直接観測されずに、出力のみが観測されます。
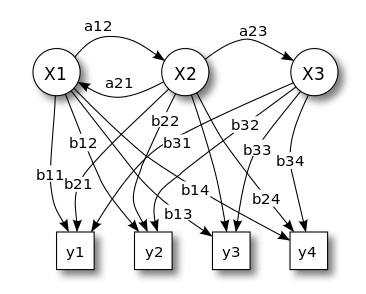
引用: https://ja.wikipedia.org/wiki/%E9%9A%A0%E3%82%8C%E3%83%9E%E3%83%AB%E3%82%B3%E3%83%95%E3%83%A2%E3%83%87%E3%83%AB
上の図は少し複雑ですが、隠れマルコフモデルを表現しています。
- Xは潜在変数の状態、つまり、観測されていない隠れた状態を表現している
- Yは観測値を表している
- aは状態遷移の遷移確率
- bは出力確率
をそれぞれ表していて、この場合、潜在変数の状態は3つあり、また、それに対して、4つの観測値がある事になり、それぞれの状態への遷移確率、及び出力への出力確率を表しています。
一見複雑そうに見えますが、概念が理解できてしまえば、実際はそこまで複雑ではありません。
なお、隠れマルコフモデルは、前述のように音声認識に用いられる他、バイオインフォマティクスや、形態素解析、楽譜追跡等、様々な用途で幅広く使用されています。
音声認識と隠れマルコフモデルに関しては、音声認識の仕組みと、隠れマルコフモデル(HMM) もご参照ください。
3-4.ビタビアルゴリズムと、有限オートマトン
さて、既に有限オートマトンについて説明しましたが、ビタビアルゴリズムも、有限オートマトンを仮定しています。
つまり、状態数は非常に膨大であっても、それらはリストアップする事が可能であり、各状態はノードとして表現されています。
ノードには、必ず開始点と終点があるとして、その途中に経由するノードには、複数の経路が考えられる訳ですが、その中で最も生存確率が高いパス(survivor path)を選択する事が、ビタビアルゴリズムの役割となります。
ビタビアルゴリズムは、ある状態に達するためのすべての経路を探索して、それを状態の並びに対して、逐次適用するため、ある特定の経路を保持しておく必要はありません。
ビタビアルゴリズムにおいて、重要な前提の1つは、あるノードから、別のノードに遷移する際に、その増分を付与する事で、通常、その増分は数として表されます。
また、ビタビアルゴリズムが経路探索を行う際に、先ほど説明した増分は、どんどん経路に蓄積されていくと考えます。
これがどのような意味かというと、新たな事象が発生した場合に、ビタビアルゴリズムは、今までの状態経路が保持していた値と、新たな状態に遷移する際の増分を考慮して、最も良いものを選択するように振る舞います。
3-5.ビタビアルゴリズムの具体例
ビタビアルゴリズムの概要について解説して参りましたが、正直、文章を読んでいるだけではよくわからない、と思っている方が多いのかと思います。
ですので、これからわかりやすい例を取り上げて解説を進めていきます。
ある遠くに住んでいる知人と連絡をとっていて、その人とLineで毎日連絡を取る事とします。
その人は、所謂ひきこもりで、毎日、「寝る」「ゲーム」「食べる」しか、行動をせず、そのうちのどれかの行動を報告してくれます。
彼が何をするかは、その日の天気だけに依存するものとし、また、彼の住んでいる場所の天気は、傾向はわかっているけども、知る術はないとして、この場合に、彼の行動から、彼の住んでいる場所の天気を予測してみましょう。
その地域の天気は、傾向はわかっていますが、我々が知る事ができないため、我々にとっては隠された状態になっています。
つまり、これは隠れマルコフモデルで言う、潜在変数に対応し、毎日、友人はLineで、「寝る」「ゲーム」「食べる」のうちのどれかの行動を報告してくるため、その行動は観測されている状態になっているので、これは隠れマルコフモデルでの出力値となっています。
さて、この隠れマルコフモデルをpythonで表現すると、以下のようになります。
states = ('Rainy', 'Sunny', 'Cloudy')
observations = ('sleep', 'game', 'eat')
start_probability = {'Rainy': 0.3, 'Sunny': 0.4, 'Cloudy': 0.3}
transition_probability = {
'Rainy' : {'Rainy': 0.4, 'Sunny': 0.3, 'Cloudy': 0.3},
'Sunny' : {'Rainy': 0.2, 'Sunny': 0.7, 'Cloudy': 0.1},
'Cloudy' : {'Rainy': 0.4, 'Sunny': 0.1, 'Cloudy': 0.5}
}
emission_probability = {
'Rainy' : {sleep: 0.4, 'game': 0.4, 'eat': 0.1},
'Sunny' : {'sleep': 0.2, 'game': 0.7, 'eat': 0.1},
'Cloudy' : {'sleep': 0.2, 'game': 0.2, 'eat': 0.6},
}
引用: https://ja.wikipedia.org/wiki/%E3%83%93%E3%82%BF%E3%83%93%E3%82%A2%E3%83%AB%E3%82%B4%E3%83%AA%E3%82%BA%E3%83%A0
- statesは、潜在変数を表している
- observationsは、出力値を表しています
- start_probabilityは、一番最初に知人がLineをしてきた際の、天気の状態を表している
- transition_probabilityは、状態遷移の確率を表している
- emission_probabilityは、出力値の確率値を表している
隠れマルコフの説明がしっかりと理解できているようであれば、上記のコードを理解するのは、さほど難しくないかと思います。
さて、それでは、この隠れマルコフモデルを用いて、知人の地域の天気を予測してみましょう。
ここは、読者の皆様に色々な仮定をして、実際に以下に示すforward_viterbiのアルゴリジムで計算を行って頂きたいところですが、設定として例えば、三日間連続で、知人とLineで話をしたところ、最初の2日間はゲームをし、最後の1日は寝ていたとの事です。
それでは、この観測結果(出力)全体の繋がりの確率はどうなったか?
また、この観測結果(出力)を説明するのに、最尤な天気の確率(遷移確率)の繋がりはどうなったか?
これを求める事が、その地域の天気を求める事で、前者は、「前向きアルゴリズム」、後者は「ビタビアルゴリズム」によって求める事ができます。
これら2つのアルゴリズムは、構造的に非常に近く、1つの関数として、実装可能で、その実装例を示します。
勿論、これ以外の課題設定を皆様が設定し、色々結果を試してみる事をおすすめします。
def forward_viterbi(y, X, sp, tp, ep):
T = {}
for state in X:
## prob. V. path V. prob.
T[state] = (sp[state], [state], sp[state])
for output in y:
U = {}
for next_state in X:
total = 0
argmax = None
valmax = 0
for source_state in X:
(prob, v_path, v_prob) = T[source_state]
p = ep[source_state][output] * tp[source_state][next_state]
prob *= p
v_prob *= p
total += prob
if v_prob > valmax:
argmax = v_path + [next_state]
valmax = v_prob
U[next_state] = (total, argmax, valmax)
T = U
## apply sum/max to the final states:
total = 0
argmax = None
valmax = 0
for state in X:
(prob, v_path, v_prob) = T[state]
total += prob
if v_prob > valmax:
argmax = v_path
valmax = v_prob
return (total, argmax, valmax)
引用: https://ja.wikipedia.org/wiki/%E3%83%93%E3%82%BF%E3%83%93%E3%82%A2%E3%83%AB%E3%82%B4%E3%83%AA%E3%82%BA%E3%83%A0
foward_viterbi関数の引数に関して説明すると、以下のようになります。
- yは、観測された行動のシーケンスを表し、上記の例では [“game”, “game”, “sleep”]
- Xは潜在変数で、隠れマルコフモデルのstatesに当たる
- spは、初期確率で、隠れマルコフモデルのstart_probability
- tpは、遷移確率で、隠れマルコフモデルのtransition_probability
- epは、状態遷移確率で、隠れマルコフモデルのemission_probability
少し、説明無しには理解が複雑なアルゴリズムに見えると思いますが、
このアルゴリズムはTとUという変数のマッピングを使い、
これらは (prob, v_path, v_prob) へのマッピングとなり、
probは、初期状態から、現在の経路までの全ての経路の確率で、
v_pathは現在の状態までのビタビ経路です。
v_probは、現在の経路までのビタビ確率を表しています。
Tは、上記3つの情報(prob, v_path, v_prob)を時刻Tで保持していて、Uは、時刻t+1いおいて、同等の情報を保持しています。
マルコフ過程に従うので、過去の情報は不要になるため、時刻t以前の情報は不要となります。
このアルゴリズムは、まずTを初期の確率で初期化を行います。
T[state] = (sp[state], [state], sp[state])メインのfor loopでは、Yから順に観測結果を取り出していきます。
for output in y:Tはその時刻での正しい情報を含むが、現在の観測時点での情報は含んでいないので、このアルゴリズムは次に、(prob, v_path, v_prob)について考えられる値をそれぞれ計算していきます。
ここから、だんだん複雑さがましていきますが、ここからが、「前向きアルゴリズム」及び「ビタビアルゴリズム」の核になります。
for loopが幾つも入れ子構造になっていて、複雑ですが、これはその状態に到達するための全経路の確率の総和を計算するためのものです。
言い方を変えると、このアルゴリズムは、考えられる全ての元の状態について繰り返しています。
それぞれの元の状態に対して、Tは、その状態に達する、全経路の全体確率を保持していて、そのTに、ある事象が得られる出力確率と、次の状態に遷移する、遷移確率を掛け合わしたものを、totalに加算します。
(prob, v_path, v_prob) = T[source_state]
p = ep[source_state][output] * tp[source_state][next_state]
prob *= p
v_prob *= p
total += prob
ビタビの経路の確率も同様に計算できますが、その場合、以下のif文からわかると思いますが、全経路の全体確率を保存するのでなく、その中で、最大の確率を保存するようにします。
これが最尤パス検索のアルゴリズムの核となります。
valmaxの初期値は0で、常に経路の確率値が、現在のvalmaxを上回った際に更新されます。
また、ビタビ経路そのものは、常に最尤の確率に対応した状態遷移を保持をargmaxに保持するようにします。
if v_prob > valmax:
argmax = v_path + [next_state]
valmax = v_prob
そうやって、以下のように、次のように、全経路の全体確率、ビタビ経路の状態遷移、ビタビ経路の確率が、計算された段階で、Uに格納します。
U[next_state] = (total, argmax, valmax)そして、それが全てのUの可能な状態で、計算されるとTに代入されます
T = U全ての経路の探索が終わった後に、以下のように、格納された値の、総和と、最大をとり、このアルゴリズムは完結となります。
## apply sum/max to the final states:
total = 0
argmax = None
valmax = 0
for state in X:
(prob, v_path, v_prob) = T[state]
total += prob
if v_prob > valmax:
argmax = v_path
valmax = v_prob
return (total, argmax, valmax)
さて、少し複雑なアルゴリズムになりましたが、隠れマルコフモデルさえ、正しく構築できてしまえば、その中で行われる処理としては、さほど難しいものではないです。
