※サンプル・コード掲載
あらすじ
機械学習の本質はデータ中のパターンを認識することです。
これを突き詰めるとデータ、ソフトウェア、そして数学的処理の3つの要素となります。
しかし、たった7行のコードで何ができるでしょう?
多くのことができます。
数行のコードでディープラーニングの問題を減らすためには「フレームワーク」を使います。
今回はTensorFlowとtflearnを使います。
抽象化は、ソフトウェアにおいて大変重要な要素です。
このページを見るためにあなたが使っているアプリケーションは、ファイルの読み込みや画像の表示等を行うオペレーション・システム上にある抽象化レイヤーです。
究極的にはビットを動かすCPUレベルのコード、つまりベアメタルがあります。
ソフトウェアのフレームワークは抽象化レイヤーです。
TensorFlowの上位層であるtflearnを使い問題を減らすことができます。
そして、TensorFlowはPythonの上位層です。
効率よく作業するためにiPython notebookを使っていきます。
以下の記事で、私たちはPython(フレームワーク無し)を使ってニューラルネットワークを作りました。
 【入門】ニューラルネットワークの仕組み
【入門】ニューラルネットワークの仕組み
そして機械学習がどのようにデータパターンから学習するかをお見せしました。
サンプルデータを呼び出すことはとてもシンプルなので、その中のパターンを直感的に理解できます。
この抽象化のコードのはこちらです。
モデル中のそれぞれの数学的処理が詳しく示されています。
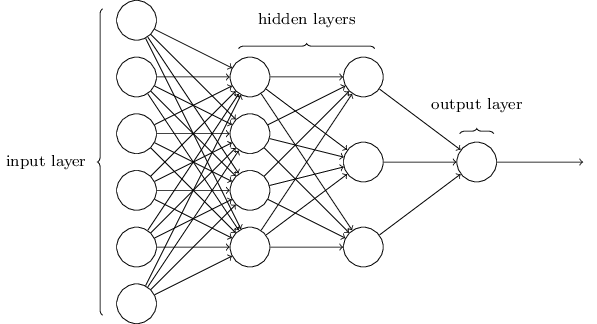
2つの内面層と、テキスト解析のために作った最急降下法(Gradient Descent)を使うために私たちのモデルを拡張すると、再びフレームワークなしの、80行以内のコードができます。
これはディープラーニングの一例で「深さ」は内部の隠れた層から来ます。
このモデルの定義づけは比較的簡単で、ほとんどのコードはトレーニングに適用されます。
# convert output of sigmoid function to its derivative
def sigmoid_output_to_derivative(output):
return output*(1-output)
def think(sentence, show_details=False):
x = bow(sentence.lower(), words, show_details)
if show_details:
print ("sentence:", sentence, "\n bow:", x)
# input layer is our bag of words
l0 = x
# matrix multiplication of input and hidden layer
l1 = sigmoid(np.dot(l0, synapse_0))
# output layer
l2 = sigmoid(np.dot(l1, synapse_1))
return l2
def train(X, y, hidden_neurons=10, alpha=1, epochs=50000, dropout=False, dropout_percent=0.5):
print ("Training with %s neurons, alpha:%s, dropout:%s %s" % (hidden_neurons, str(alpha), dropout, dropout_percent if dropout else '') )
print ("Input matrix: %sx%s Output matrix: %sx%s" % (len(X),len(X[0]),1, len(classes)) )
np.random.seed(1)
last_mean_error = 1
# randomly initialize our weights with mean 0
synapse_0 = 2*np.random.random((len(X[0]), hidden_neurons)) - 1
synapse_1 = 2*np.random.random((hidden_neurons, len(classes))) - 1
prev_synapse_0_weight_update = np.zeros_like(synapse_0)
prev_synapse_1_weight_update = np.zeros_like(synapse_1)
synapse_0_direction_count = np.zeros_like(synapse_0)
synapse_1_direction_count = np.zeros_like(synapse_1)
for j in iter(range(epochs+1)):
# Feed forward through layers 0, 1, and 2
layer_0 = X
layer_1 = sigmoid(np.dot(layer_0, synapse_0))
if(dropout):
layer_1 *= np.random.binomial([np.ones((len(X),hidden_neurons))],1-dropout_percent)[0] * (1.0/(1-dropout_percent))
layer_2 = sigmoid(np.dot(layer_1, synapse_1))
# how much did we miss the target value?
layer_2_error = y - layer_2
if (j% 10000) == 0 and j > 5000:
# if this 10k iteration's error is greater than the last iteration, break out
if np.mean(np.abs(layer_2_error)) last_mean_error:
print ("delta after "+str(j)+" iterations:" + str(np.mean(np.abs(layer_2_error))) )
last_mean_error = np.mean(np.abs(layer_2_error))
else:
print ("break:", np.mean(np.abs(layer_2_error)), ">", last_mean_error )
break
# in what direction is the target value?
# were we really sure? if so, don't change too much.
layer_2_delta = layer_2_error * sigmoid_output_to_derivative(layer_2)
# how much did each l1 value contribute to the l2 error (according to the weights)?
layer_1_error = layer_2_delta.dot(synapse_1.T)
# in what direction is the target l1?
# were we really sure? if so, don't change too much.
layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1)
synapse_1_weight_update = (layer_1.T.dot(layer_2_delta))
synapse_0_weight_update = (layer_0.T.dot(layer_1_delta))
if(j > 0):
synapse_0_direction_count += np.abs(((synapse_0_weight_update > 0)+0) - ((prev_synapse_0_weight_update > 0) + 0))
synapse_1_direction_count += np.abs(((synapse_1_weight_update > 0)+0) - ((prev_synapse_1_weight_update > 0) + 0))
synapse_1 += alpha * synapse_1_weight_update
synapse_0 += alpha * synapse_0_weight_update
prev_synapse_0_weight_update = synapse_0_weight_update
prev_synapse_1_weight_update = synapse_1_weight_update
now = datetime.datetime.now()
# persist synapses
synapse = {'synapse0': synapse_0.tolist(), 'synapse1': synapse_1.tolist(),
'datetime': now.strftime("%Y-%m-%d %H:%M"),
'words': words,
'classes': classes
}
synapse_file = "synapses.json"
with open(synapse_file, 'w') as outfile:
json.dump(synapse, outfile, indent=4, sort_keys=True)
print ("saved synapses to:", synapse_file)これでうまく動作しました。
つぎは、フレームワークを使い抽象化します。
TensorFlowによる抽象化
以下の記事で、我々は同じニューラルネットワークを作り、機械学習でデータパターンからどの様に学習するのかをお見せしました。
 TensorFlow【入門】テンソルフローの使い方
TensorFlow【入門】テンソルフローの使い方
そして、コード(数学的構造)をシンプルにしました。
例えば、最急降下法の処理と関数は2行のコードに減らされています。
# formula for cost (error)
cost = tf.reduce_mean( tf.nn.softmax_cross_entropy_with_logits(prediction,y) )
# optimize for cost using GradientDescent
optimizer = tf.train.GradientDescentOptimizer(1).minimize(cost)我々のモデルの定義もまた単純化されています。
数学的関数と一般関数(例えば、シグモイド)はフレームワークの中でカプセル化されています。
# our predictive model's definition
def neural_network_model(data):
# hidden layer 1: (data * W) + b
l1 = tf.add(tf.matmul(data,hidden_1_layer['weight']), hidden_1_layer['bias'])
l1 = tf.sigmoid(l1)
# hidden layer 2: (hidden_layer_1 * W) + b
l2 = tf.add(tf.matmul(l1,hidden_2_layer['weight']), hidden_2_layer['bias'])
l2 = tf.sigmoid(l2)
# output: (hidden_layer_2 * W) + b
output = tf.matmul(l2,output_layer['weight']) + output_layer['bias']
return outputAlexNetのような複雑なニューラルネットワークの「フロー」が、TensorFlow を使うことによって定義が単純化され、数学的な「フロー」の動きをしているのがイメージできるでしょう。
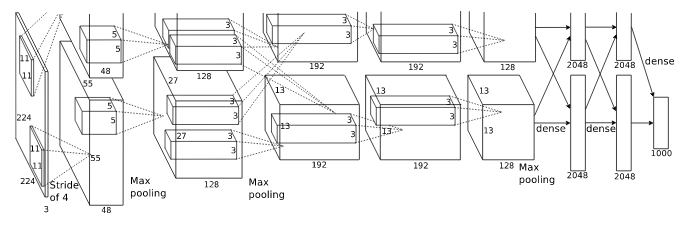
再度、抽象化
まだコードが多く複雑で満足できないので、tflearnを使い再び抽象化します。
tflearnは以下の様に定義されています。
TFLearn: TensorFlow用の高レベルのAPIを備えたディープラーニング・ライブラリ。
ここで言う高レベルとは、高度な抽象化レベルの事を指し、まさに私たちが必要とするものです。
私達は多層ニューラルネットのために7行のコードを書きます。
# Build neural network
net = tflearn.input_data(shape=[None, 5])
net = tflearn.fully_connected(net, 32)
net = tflearn.fully_connected(net, 32)
net = tflearn.fully_connected(net, 2, activation='softmax')
net = tflearn.regression(net)
# Define model and setup tensorboard
model = tflearn.DNN(net, tensorboard_dir='tflearn_logs')
# Start training (apply gradient descent algorithm)
model.fit(train_x, train_y, n_epoch=500, batch_size=16, show_metric=True)5行のコードがニューラルネット構造を定義しています。
そしてトレーニングのための2行です。
Notebookのコードはここにあります。
詳しく説明していきましょう。
データと学習の目的は私たちの以下の例と同じです。
 TensorFlow【入門】テンソルフローの使い方
TensorFlow【入門】テンソルフローの使い方
フレームワークのインストール
TensorFlow 1.0X がインストールされている事を確認してください。
TflearnのフレームワークはTensorFlow1.0以前のバージョンでは作動しません。
import tensorflow as tf
tf.__version__'1.0.1'LinuxWith pipでは以下を使うと便利かもしれません。
python -m pip install — upgrade tensorflow tflearnデータ
次のステップでは、tensorflowのサンプルデータを設定します。
 TensorFlow【入門】テンソルフローの使い方
TensorFlow【入門】テンソルフローの使い方
トレーニングデータの詳細はここで説明されており一目瞭然だと思います。
テストデータを作る必要はもうありません。
tflearnフレームワークがやってくれます。
import numpy as np
import tflearn
import random
def create_feature_sets_and_labels():
# known patterns (5 features) output of [1] of positions [0,4]==1
features = []
features.append([[0, 0, 0, 0, 0], [0,1]])
features.append([[0, 0, 0, 0, 1], [0,1]])
features.append([[0, 0, 0, 1, 1], [0,1]])
features.append([[0, 0, 1, 1, 1], [0,1]])
features.append([[0, 1, 1, 1, 1], [0,1]])
features.append([[1, 1, 1, 1, 0], [0,1]])
features.append([[1, 1, 1, 0, 0], [0,1]])
features.append([[1, 1, 0, 0, 0], [0,1]])
features.append([[1, 0, 0, 0, 0], [0,1]])
features.append([[1, 0, 0, 1, 0], [0,1]])
features.append([[1, 0, 1, 1, 0], [0,1]])
features.append([[1, 1, 0, 1, 0], [0,1]])
features.append([[0, 1, 0, 1, 1], [0,1]])
features.append([[0, 0, 1, 0, 1], [0,1]])
features.append([[1, 0, 1, 1, 1], [1,0]])
features.append([[1, 1, 0, 1, 1], [1,0]])
features.append([[1, 0, 1, 0, 1], [1,0]])
features.append([[1, 0, 0, 0, 1], [1,0]])
features.append([[1, 1, 0, 0, 1], [1,0]])
features.append([[1, 1, 1, 0, 1], [1,0]])
features.append([[1, 1, 1, 1, 1], [1,0]])
features.append([[1, 0, 0, 1, 1], [1,0]])
# shuffle our features and turn into np.array
random.shuffle(features)
features = np.array(features)
# create train and test lists
train_x = list(features[:,0])
train_y = list(features[:,1])
return train_x, train_y私達のディープラーニングコードです。
7行のコード
# Build neural network
net = tflearn.input_data(shape=[None, 5])
net = tflearn.fully_connected(net, 32)
net = tflearn.fully_connected(net, 32)
net = tflearn.fully_connected(net, 2, activation='softmax')
net = tflearn.regression(net)
# Define model and setup tensorboard
model = tflearn.DNN(net, tensorboard_dir='tflearn_logs')
# Start training (apply gradient descent algorithm)
model.fit(train_x, train_y, n_epoch=500, batch_size=16, show_metric=True)始めの5行は tflearn.input_data から tflearn.fully_connected、そして tflearn.regression へと続くtflearnの関数の配列のニューラルネットを定義しています。
このフローは私達のTensorFlowのサンプルと一致します。
すなわち入力データは5つの機能があり、それぞれの層の中の32のnodeを使い、アウトプットは2つのクラスがあります。
次にディープニューラルネットワークであるtflearn.DNNを私達のネットワークで起動させます。
tensorboard パラメーターを使いロギングします。
最後にトレーニングデータを私たちのモデルに対応させます。
トレーニングメトリックスのためのインターフェイスに注目してくだい。
精度に与える影響を見るためにn_epochsを変えてください。
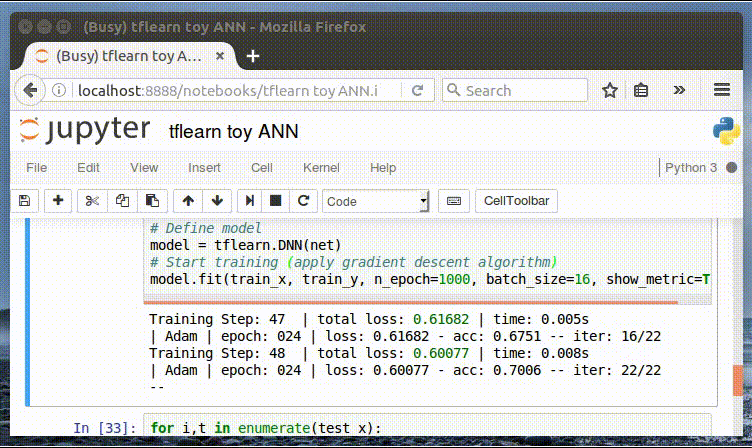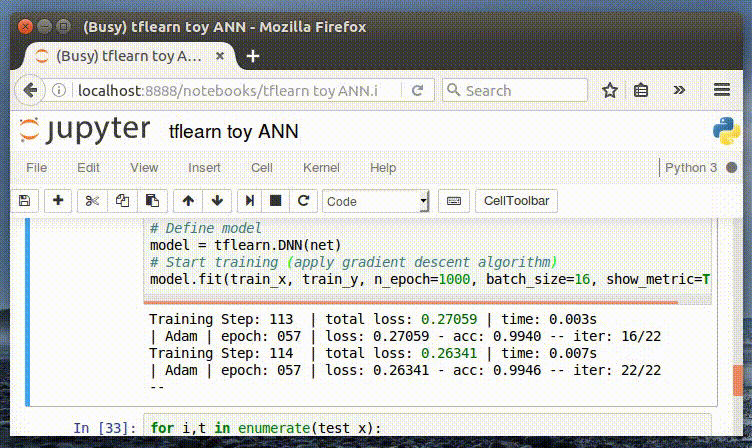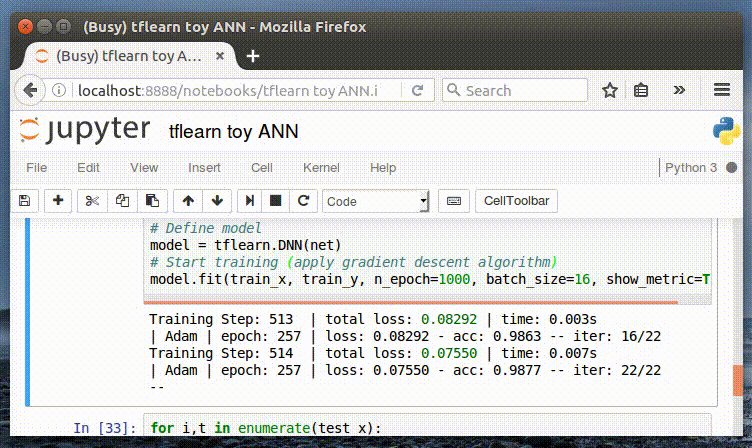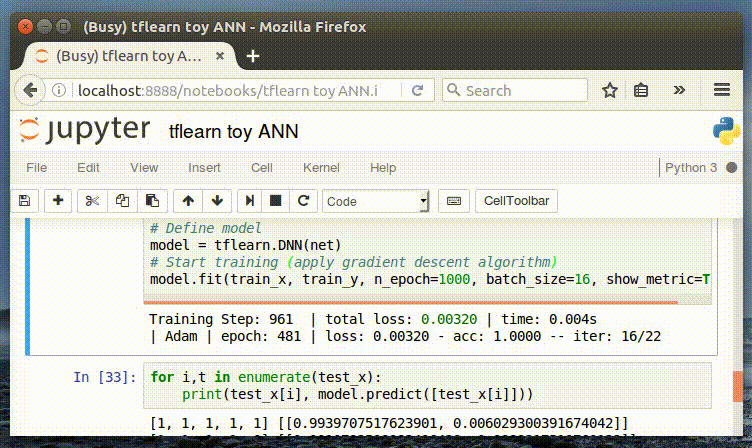
Training Step: 1999 | total loss: 0.01591 | time: 0.003s
| Adam | epoch: 1000 | loss: 0.01591 - acc: 0.9997 -- iter: 16/22
Training Step: 2000 | total loss: 0.01561 | time: 0.006s
| Adam | epoch: 1000 | loss: 0.01561 - acc: 0.9997 -- iter: 22/22
--予想
私達のモデルを使いアウトプットを予想することができるようになりました。
トレーニングデータから全てのテストパターンを削除して下さい(テストしたいパターンを含んでいる行はコメントアウトしてください)。
そうしないと、モデルが不正になります。
print(model.predict([[0, 0, 0, 1, 1]]))
print(model.predict([[1, 0, 1, 0, 1]]))[0.004509848542511463、0.9954901337623596 ]]
[[ 0.9810173511505127、0.018982617184519768]私達のモデルはアウトプット[1, 0] と[1, , , _, 1]パターンを正しく認識しています。
Notebook を反復して使うとき、モデルコードの直ぐ上に2行追加してモデルのグラフをリセットすると便利です。
# reset underlying graph data
import tensorflow as tf
tf.reset_default_graph()
# Build neural network
...抽象化することにより、我々はデータの用意とモデルを使った予想に集中できます。
Tensorboard
Tflearnフレームワークはデータをtensorboard(Tensorflow用の可視化ツール)に自動的に送ります。
tflearn.DNN でログファイルを用意したので目を通してみましょう。
$ tensorboard — logdir=tflearn_logs
Starting TensorBoard b’41' on port 6006
(You can navigate to http://127.0.1.1:6006)ここで私達の「フロー」のグラフをみることができます。
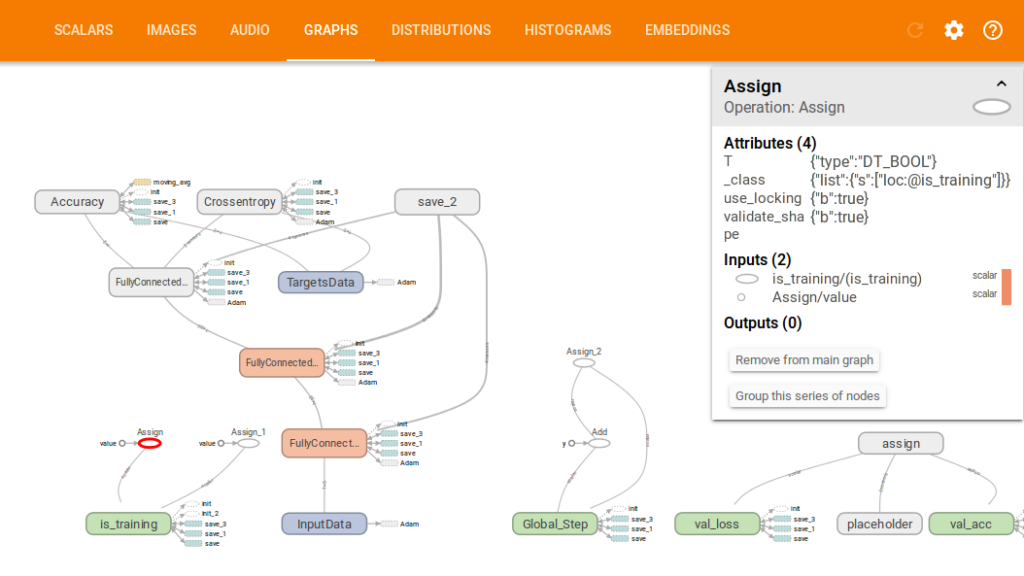
そして精度と損失関数のパフォーマンスが見られます。
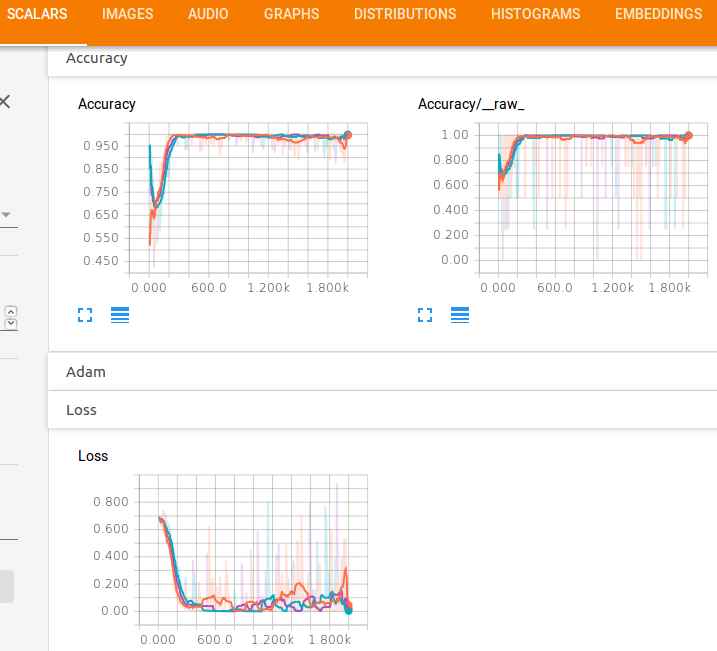
トレーニングにおいて高い精度を出すために、それほど多くのepochsが必要ないことが明らかです。
その他の例
これは LSTM RNN (Long-Short-Term-Memory Recurrent Neural-Net)、のためのtflearnのセットアップです。
これはメモリーとともにデータシーケンスを学習するのによく使われます。
ネットワークとtflearn.lstmの設定の違いに注目してください、しかしほとんどは同じ基本的なコンセプトです。
# Network building
net = tflearn.input_data([None, 100])
net = tflearn.embedding(net, input_dim=10000, output_dim=128)
net = tflearn.lstm(net, 128, dropout=0.8)
net = tflearn.fully_connected(net, 2, activation='softmax')
net = tflearn.regression(net, optimizer='adam', learning_rate=0.001,
loss='categorical_crossentropy')
# Training
model = tflearn.DNN(net)
model.fit(trainX, trainY, validation_set=(testX, testY), show_metric=True,
batch_size=32)そしてこれはConvolutional Neural Networkのためのtflearnのセットアップです。
画像認識のためによく使われます。
ここで行っている事はネットワークの数式のために数学的シーケンスを用意し、データをフィードすることです。
# Building convolutional network
network = input_data(shape=[None, 28, 28, 1], name='input')
network = conv_2d(network, 32, 3, activation='relu', regularizer="L2")
network = max_pool_2d(network, 2)
network = local_response_normalization(network)
network = conv_2d(network, 64, 3, activation='relu', regularizer="L2")
network = max_pool_2d(network, 2)
network = local_response_normalization(network)
network = fully_connected(network, 128, activation='tanh')
network = dropout(network, 0.8)
network = fully_connected(network, 256, activation='tanh')
network = dropout(network, 0.8)
network = fully_connected(network, 10, activation='softmax')
network = regression(network, optimizer='adam', learning_rate=0.01,
loss='categorical_crossentropy', name='target')
# Training
model = tflearn.DNN(network)
model.fit({'input': X}, {'target': Y}, n_epoch=20,
validation_set=({'input': testX}, {'target': testY}),
snapshot_step=100, show_metric=True, run_id='convnet_mnist')我々はフレームワーク無しのコードを学ぶことから始めました。
フレームワーク無しのコードは内部がどの様に作動しているのかを明確に表示します。
ブラックボックスはありません。
内部のコードを確実に理解し、何が起きているのかがわかったら、フレームワークを使って作業を単純化します。
ディープラーニングのフレームワークは内部機能をカプセル化して作業をシンプルにします。
フレームワークが進化し改良されるとそれらの改良点を自動的に受け継ぐので、結果的に我々はブラックボックスからブラックボックスの中にあるブラックボックスへと向かいます。
原文
https://chatbotslife.com/deep-learning-in-7-lines-of-code-7879a8ef8cfb
チャットボットライフとの提携により、翻訳し掲載しています。
チャットボットライフとは、最新のボット、AI、NLP、ツール等を扱うメディアです。
