※サンプル・コード掲載
あらすじ
人工ニューラルネットワーク(ANN)は興味深いトピックとなり、チャットボットはテキスト分類においてそれらを頻繁に使用します。
しかし、正直に言うと、あなたが神経科学者でない限り、脳をアナロジーとして説明することはないでしょう。
動物の脳内のシナプスおよびニューロンに対するソフトウェアのアナロジーは、近年になってファンタジーを生み出していきましたが(given rise to fantasy)、ソフトウェアのニューラルネットワークは数十年にわたって存在していました。
簡単なアナロジーを使って説明してみましょう:弦楽器
チューニング方法
人工のニューラルネットワークは“チューニング”された弦楽器の集合体のようなものです。
ギターと特定のコードに合わせるために弦楽器をチューニングする過程を想像してください。
それぞれの弦はしっかりと閉められるにつれて、特定の音調に、より“チューンの合った”状態になります。
その締め付けの強さは、他の弦の調整を必要にさせます。
これを繰り返し行うことで、その度にピッチのエラーは減少し、最終的に適切にチューニングされた楽器となるのです。
一連のチューニングペグ(neurons) に接続された、それぞれの弦(synapse)の締め付け具合、そして正しいチューニングのためのイテレーションの過程(training data)を想像してください。
それぞれのイテレーションにおいて、好ましいピッチにアジャストするための追加の微調整が存在します(back-propagation)。
最終的に楽器はチューニングされ、演奏の際(used for prediction)、正しく調和するのです(許容範囲内のエラーレートで)。
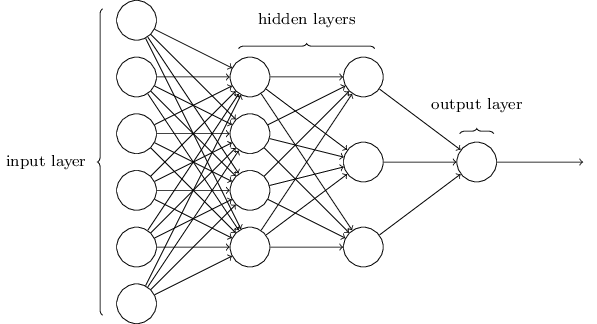
多層ニューラルネットワーク
ソフトウェアにおいて“おもちゃ”の人工ニューラルネットワークを構築してみましょう。
私たちのサンプルのコードはこちらです。
PythonとiPythonを使用します。いつものように“ブラックボックスなし”のアプローチを使用することで、どのようにその装置が機能しているのかを理解することができます。
非常にシンプルなトレーニングデータセット、一連の3つのバイナリデータおよび出力を提供します。
input [ 0, 0, 1 ] output: 0
input [ 1, 1, 1 ] output: 1
input [ 1, 0, 1 ] output: 1
input [ 0, 1, 0] output: 0
出力が最初の値と同数である点に(上記の太字部分に)注意してください。
例えば、[ 1, 1, 0]の出力が何であるかはわかりませんが、トレーニングデータのパターンは出力が1であると強く示唆しています。
これがパターンです。
人間の知性の核は、パターンに対する感受性である
numpy を使用して、トレーニングデータをリストの配列として表現します。
import numpy
# The training set. We have 4 examples, each consisting of 3 input values
# and 1 output value.
training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 0]])
training_set_outputs = array([[0, 1, 1, 0]]).T
次に、init関数からクラス内のニューラルネットワーク関数を定義します。
class NeuralNetwork():
def __init__(self):
# Seed the random number generator, so it generates the same numbers
# every time the program runs.
random.seed(1)
# We model a single neuron, with 3 input connections and 1 output connection.
# We assign random weights to a 3 x 1 matrix, with values in the range -1 to 1
# and mean 0.
self.synaptic_weights = 2 * random.random((3, 1)) - 1
クレジットAndrew Trask https://iamtrask.github.io//2015/07/12/basic-python-network/
シナプス荷重はランダムな数値として始まり、3×1のネットワークの寸法がトレーニングデータ(例[0, 1, 0])と矛盾しないことに注意してください。
Random starting synaptic weights:
[[-0.16595599]
[ 0.44064899]
[-0.99977125]]
次に値を正常化する関数を定義します。
# The Sigmoid function, which describes an S shaped curve.
# We pass the weighted sum of the inputs through this function to
# normalise them between 0 and 1.
def __sigmoid(self, x):
return 1 / (1 + exp(-x))
# The derivative of the Sigmoid function.
# This is the gradient of the Sigmoid curve.
# It indicates how confident we are about the existing weight.
def __sigmoid_derivative(self, x):
return x * (1 - x)
私たちは結果を小さく、管理しやすい数字、この場合0から1に正常化する方法が必要です。
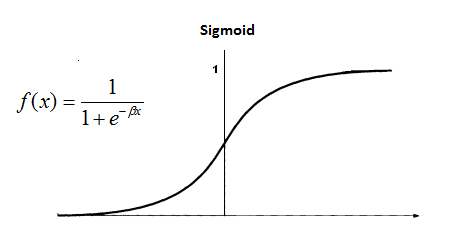
シグモイド関数がそれを処理します。
この“グラディエント”や“シグモイド導関数”はどの点においても曲線の傾きを私たちに示します。
これは私たちがどれくらい“チューンのあった”状態から“かけ離れている”(エラー)かを理解するために役立ちます。
これをギターのチューナーのようなものだと考えてください。
それは、私たちが相対的に特定の音調とどのくらい“ずれている”かを教えてくれるのです。
これで私たちのネットワークをトレーニング(チューン)する準備が整いました。
# We train the neural network through a process of trial and error.
# Adjusting the synaptic weights each time.
def train(self, training_set_inputs, training_set_outputs, number_of_training_iterations):
for iteration in iter(range(number_of_training_iterations)):
# Pass the training set through our neural network (a single neuron).
output = self.think(training_set_inputs)
# Calculate the error (The difference between the desired output
# and the predicted output).
error = training_set_outputs - output
# Multiply the error by the input and again by the gradient of the Sigmoid curve.
# This means less confident weights are adjusted more.
# This means inputs, which are zero, do not cause changes to the weights.
adjustment = dot(training_set_inputs.T, error * self.__sigmoid_derivative(output))
# Adjust the weights.
self.synaptic_weights += adjustment
if (iteration % 1000 == 0):
print ("error after %s iterations: %s" % (iteration, str(numpy.mean(numpy.abs(error)))))
ここで起きている全てのこと(実際には6行のコード)は行列の乗算(matrix multiplication)であり、中学数学で学んだことです。
エラーレート(ピッチの不一致レベル)が1,000回のイテレーションごとに着実に減少していることがわかり、合計で10,000回のイテレーション後、動作を行う上で十分に少ないエラーにとなっています。
error after 1000 iterations: 0.0353771814512
error after 2000 iterations: 0.024323319584
error after 3000 iterations: 0.0196075022358
error after 4000 iterations: 0.016850233908
error after 5000 iterations: 0.014991814044
error after 6000 iterations: 0.0136320935305
error after 7000 iterations: 0.01258242301
error after 8000 iterations: 0.0117408289409
error after 9000 iterations: 0.0110467781322
演奏した時にチューンの外れた楽器に対して敏感になり過ぎるように、ネットワークを厳密にチューニングし過ぎることは役に立たないということに注意してください。
必要最低限のイテレーション数は、通常、トレーニングデータの大きさに関係します。
私たちは考えすぎて、感じなさ過ぎる
次のセクションは私のお気に入りです:“思考”を行うコードの1行です。
sigmoid( dot ( inputs, synaptic_weights))
# The neural network 'thinks'
def think(self, inputs):
# Pass inputs through our neural network (our single neuron).
return self.__sigmoid(dot(inputs, self.synaptic_weights))
入力と重さのドット積(行列乗算)のために正常化された値。
このことからニューラルネットワークの“思考”(より正確に“予測”する)が結果であるという、私たちの結果と予測を得ました。
待って、それは...?
それはいわゆる“人工知能”ですか?
少なくとも、0と1のストリーミングを見ることができ、それは事実です。
私たちが今する必要がある全てのことは、メインセクションを整理し、例を実行することです。
if __name__ == "__main__":
#Intialise a single neuron neural network.
neural_network = NeuralNetwork()
print ("Random starting synaptic weights: ")
print (neural_network.synaptic_weights)
# Train the neural network using a training set.
# Do it 10,000 times and make small adjustments each time.
neural_network.train(training_set_inputs, training_set_outputs, 10000)
print ("New synaptic weights after training: ")
print (neural_network.synaptic_weights)
# Test the neural network with a new pattern
test = [1, 0, 0]
print ("Considering new situation %s -> ?: " % test )
print (neural_network.think(array(test)))
Random starting synaptic weights:
[[-0.16595599]
[ 0.44064899]
[-0.99977125]]
error after 0 iterations: 0.578374046722
error after 1000 iterations: 0.0353771814512
error after 2000 iterations: 0.024323319584
error after 3000 iterations: 0.0196075022358
error after 4000 iterations: 0.016850233908
error after 5000 iterations: 0.014991814044
error after 6000 iterations: 0.0136320935305
error after 7000 iterations: 0.01258242301
error after 8000 iterations: 0.0117408289409
error after 9000 iterations: 0.0110467781322
New synaptic weights after training:
[[ 12.79547496]
[ -4.2162058 ]
[ -4.21608782]]
Considering new situation [1, 0, 0] -> ?:
[ 0.99999723]
ここで何が起きたのか?
私たちは4つのトレーニングパターンから始めました:
input [ 0, 0, 1 ] output: 0
input [ 1, 1, 1 ] output: 1
input [ 1, 0, 1 ] output: 1
input [ 0, 1, 0] output: 0
次に私たちは、ニューラルネットワークに[1, 0, 0]の出力を予測するように訪ね、それは0.99の値を導き出しました。
それは実質的には1の出力です。
未知の出力を持つ他の値のセットを与えてみましょう:
Considering new situation [0, 0, 0] -> ?:
[ 0.5]
このケースにおいて、出力は0.5、つまり0ではないがそれに近い出力であると“思考しました”。
私たちはより多くのトレーニングデータと、おそらく、より多くのイテレーションが必要でしょう。
このアプローチで興味深いことは、ソフトウェアがパターンのコード“ルール”なしに有用な予測を導き出したということです。
私たちはとても簡単に以下のコードを書くことができました:
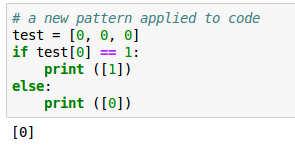
しかし、これは当然特定のパターン“ルール”があらかじめ理解されていると過程しています。
それはしばしば実用的ではありありません。
ディープラーニング
大量のデータを持つ実際の分類器では、ネットワークの大きさはより重要です。
500×7500の行列乗算、100k以上の反復と複数のニューロン層を“チューン”することを想像してください。
これは、いわゆる“ディープラーニング”です。この“深さ”はレイヤーと関係があります。
このコード例を実行してください。
一番下のボーナスセクションに、それぞれ行列と1回のイテレーション後の調整が表示されていることに注目してください。
原文
https://chatbotslife.com/how-neural-networks-work-ff4c7ad371f7
チャットボットライフとの提携により、翻訳し掲載しています。
チャットボットライフとは、最新のボット、AI、NLP、ツール等を扱うメディアです。
