あらすじ
機械学習に関しての勉強はどうやって始めればいいのか?とよく聞かれることがあります。
ほとんどの人は物事の基礎となる数学を理解することに苦戦します。
そして、私も数学が嫌いな内の一人です。
数学は物事を抽象的に表現し、機械学習も同様にとても抽象的に表現されるので簡単に理解することは難しいでしょう。
ですので、この記事では少しのJavaScriptを用いて出来るだけ簡単に説明を記述しようと思います。
あなた自身が順を追いながら実際に作業ができるように、私が全てをまとめたGitHubのリポジトリも用意するつもりです。
まず、あなたが知らないといけないことは、多様なコンセプトがあるということです。
大抵の問題は時間依存のデータ(RNNとRNN LSTM)、視覚的またはピクセルに関連したデータ(CNN)と簡単なベクトル化データ(BBN、BN、BNN、QNN)に分けられます。
ところが、工学と生物学の観点から見てみるともっと複雑な構造があり、それらは低レベルの機械学習ソリューションと自由に組み合わせることができるので、強力なツールセットとして使用できるのです。
これらのコンセプトの大半は自然言語処理(NLP)や複雑な文章の構文解析、美術的な絵画といったもっと偶然的な分野で適用されるので、この段階でこれら全てを説明する必要はないでしょう。
尚、ここでは専門的な用語やフレームワークの使用を極力避けるようにします。
簡単なES2017のJavaScriptを使ったデモコードも書いてありますので、それらを気軽に試してみたりデモをいじったりできます。
ここで最初に触れておきたい内容はニューラルネットワークと遺伝的プログラミングと進化の基本です。
ニューラルネットワークの基本
ニューラルネットワークはそれほど分かりにくいものではありません。
ただ説明が初心者向けではないということです。
他の方々は数学を使って説明を行うので、私は別の方法を使いたいと思います。
単純なニューラルネットワークに焦点を当てれば、それはいつも入力層(input layers)、非表示層(hidden layers)、出力層(output layers)という三つの異なる「カテゴリー」によって構成されています。
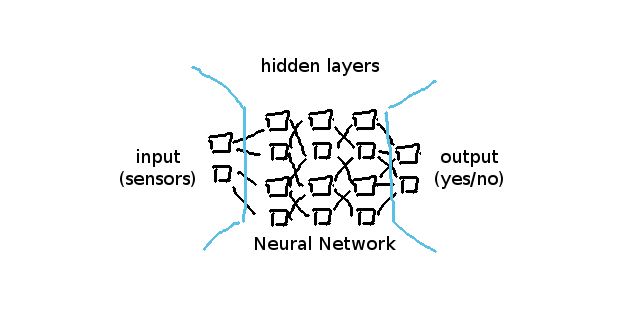
一般的に入力層は配列の各入力値が0.0から1.0までとなるセンサーのことを表します。
一般的にはそれをベクトルと呼ぶことを好んでいますが、私はそれらを値を持つ配列と呼びます。
一般的な出力層はyes/noタイプの質問への回答や、他の使い方の場合はベクトル化された性質を表します。
その性質はenumから位置オブジェクト(X,Y,Zベクトル)までの様々なことに応用できます。
重要なのはニューラルネットワークが複雑な関数やベイズ推定の限界点までを判定することができるということです。
ニューラルネットワークは単純なので、0.0から1.0までの値しか理解できません。
つまり、ニューラルネットワークがデータの意味を理解できるように、私たちはアダプターを書かなければなりません。
このアダプターの機能は数値を0.0~1.0の範囲に変換することであり他の役割はありません。
一般的な実装になると、他のニューラルネットワーク構造で再利用ができるという点から、センサーまたはコントロールと呼ばれる傾向があります。
例えば、卓球ゲームのラケットのピクセル位置を分析する場合私たちはこのような物を使います。
let input = [ 0, 0, 0 ]; // x,y,z
input[0] = entity.position.x / screen.width;
input[1] = entity.position.y / screen.height;
input[2] = 0; // we don't have a z position, have we?
let answer = neural_network.compute(input);
if (answer[0] > 0.5) {
entity.moveUpwards();
} else {
entity.moveDownwards();
}ニューラルネットワークが入力されたデータを計算し、質問への回答のようなアウトプット(>0.5だと、はい、他のはいいえ)や、私たちのシミュレーション世界への変換可能なデータオブジェクト(output = [0.5, 1.0, 0.99 ] は位置座標になる) を見せてくれたことがわかりました。
ニューラルネットワーク自体は以前に紹介した多様なニューロンを含んだ層によって構造さていれます。
単純なフィード・フォーワード・ネットワークはそれぞれ全てのニューロンが前の層のそれぞれ全てのニューロンと結びついていて、左の入力層から右の出力層までを反復するという形で構築されています。
それらの接続と活動はいわゆるウェイトで表され、ウェイトは大抵一つのニューロンの接続を表しています。
ここで重要なのは、入力ニューロンは前の層との接続がないことです。
したがって、私たちが実装で用いるcompute() メソッドでは入力ニューロンが入力配列の値と共にそれらのneuron.valueを直接的に取得することを計算に入れないといけないということです。
ニューロンはどうやって通信しているか、時間の経過とともにてウェイトはどのように変わるか、ネットワーク内の次のニューロンをいつ起動するかということはいわゆるアクティベーション・ファンクション(活性化関数)と呼ばれます。
現在、アクティベーション・ファンクションの定義には様々な意見があり少々曖昧です。
以下はシグモイド活性化関数の例です。
const _sigmoid = function(value){
return(1 /(1 + Math.exp((-1 * value)/ 1)));
};大切なことは、アクティベーション・ファンクションがニューロンの働きをシミュレートするアイデアであるということです。
実際のアクティベーション・ファンクションはある値(正式に言えば値の総計)を抽出して他の値に変換することに過ぎず、この動作はユーザーインターフェイスとアニメーションの世界における ease out または ease-in-out tweening に似ています。
オーバーフィッティングはより複雑な話題になるので、時間の節約と混乱を避けるためにこのテーマを無視することにします。
あなたに知って欲しいことは、 畳み込みニューラルネットワーク(CNN)が最初の2つのエージェントシステムを使用し、一つ目のニューラルネットワークが偽物のデータを作り、二つ目はそのデータが偽物かどうかを判断しようとするものです。
両方の強度が増すにつれ、現実世界の物事を分類することでは大変優れた成果を出すようになります。
現実世界の出来事に例えてみると、紙幣を偽造する人の技術が上がれば上がるほど銀行で作られる紙幣の模様が緻密になっていくという過程に似ています。
(少なくとも現代国家ではこうなります。)
しかしながら、進化的なANN派の私にとってそれは退屈で新たらしいものではありません。
マルチエージェント・システムの中でAIに競争をさせるアイデア自体は古いのですが、ニューラルネットワークの行動を発展さる非常に強力なアイデアであることは知っておかなければなりません。
遺伝的プログラミングと進化論
遺伝的プログラミングというのはデータをゲノムに例えるアイデアのことです。
遺伝的プログラミングの大きな長所は進化的アルゴリズムと組み合わせることで、素早くそしてかなりいい結果が出るところです。
基本的な進化アルゴリズムは訓練、評価、繁殖の三つの動作を繰り返すサイクルを持っています。
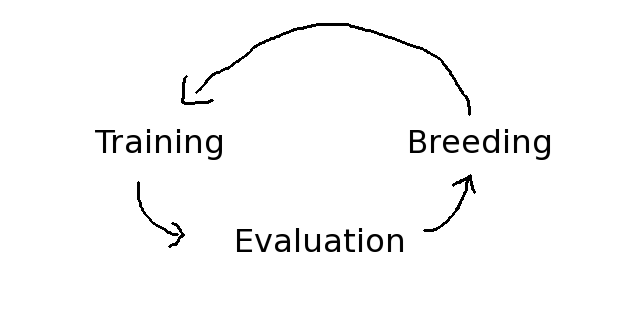
進化が常に母集団のプールから成り立っているおり、初期段階ではランダムな値を持つニューラル・ネットワークで満たされていて、それ故あなたは素早く結果を得ることが出来ます。
それらのニューラル・ネットワークはお互いに競争し合うことから一般的にエージェントと呼ばれます。
もちろん、「完璧な値」を得るためにランダムさにこだわることは少々馬鹿らしく、数学的な視点で考えれば永遠に続きます。
ですので、代わりに適性測定というものがあります。この適性は各エージェントとゲノムにとっての進捗値とすることができます。
スーパーマリオのゲームに例えると左への距離や何か得点の様なものや倒した敵の数は適性値として使うことができる。
エージェントの適合が進むと他の適合可能なエージェントと繁殖されやすくなります。
より適合したエージェントは父と母が持つ優性の遺伝子のアイデアを使っていつも二人の赤ちゃんを作ります。
そうすることで、一方は母により似た赤ちゃん(娘)になり、もう一方は父により似た赤ちゃん(息子)になり、両方の知識が将来のサイクルの中で改良される機会を持つことになります。
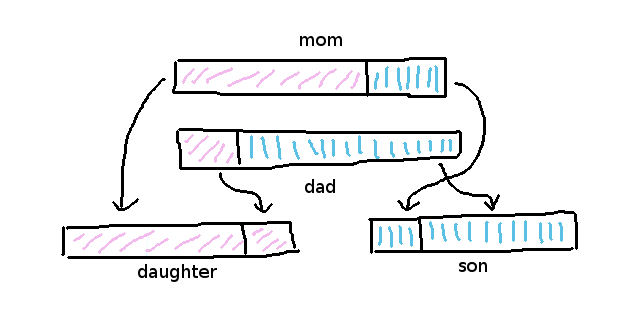
クロスオーバー・アルゴリズムは一般的にゲノムを分割する場所をランダム化します。
つまり、ゲノムが一度ランダム化され、娘は一つの部分(70% mum / 30% dad) を取得した時、息子が残りの部分(30% mum / 70% dad) を取得するということになります。
let dna_split = (Math.random() * mum_genome.length) | 0;
let daughter = new Genome();
let son = new Genome();
for (let d = 0; d mum_genome.length; d++) {
if (d > dna_split) {
son[d] = mum_genome[d];
daughter[d] = dad_genome[d];
} else {
daughter[d] = mum_genome[d];
son[d] = dad_genome[d];
}
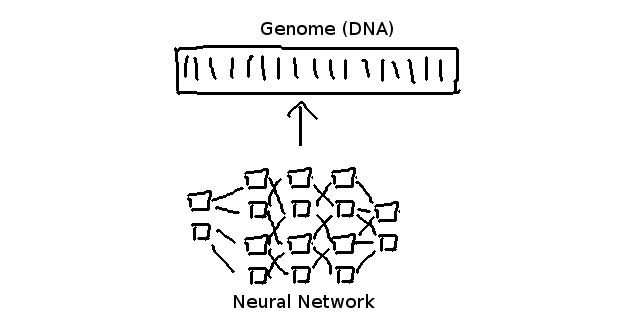
}各ゲノムが表す値は一般的にニューラル・ネットワークのウェイト値を表します。
ニューラル・ネットワークのウェイトが何なのかということは後ほど学びます。
今ご理解頂くのは、ニューラル・ネットワークの「内容」は「巨大なゲノム配列」で表現されるということです。
ニューラルネットワークのそれぞれのウェイトはゲノム配列の中に同等の「細胞」を持ちます。
しかし、典型的な進化の問題は時系列で比較してみると、時間が経過するほどに結果が向上していくとは限らないことです。
殆どの原因は一定の突然変異の発生率に起因し、それがより良いイノベーションを生み出すためには高すぎるということです。
初期段階では高い突然変異の発生率はむしろ望むべき良いことで、短期間で「それなりに良い」結果を出します。
その後、高い突然変異の発生率が悪影響を及ぼし、生み出すイノベーションの量を減少させます。
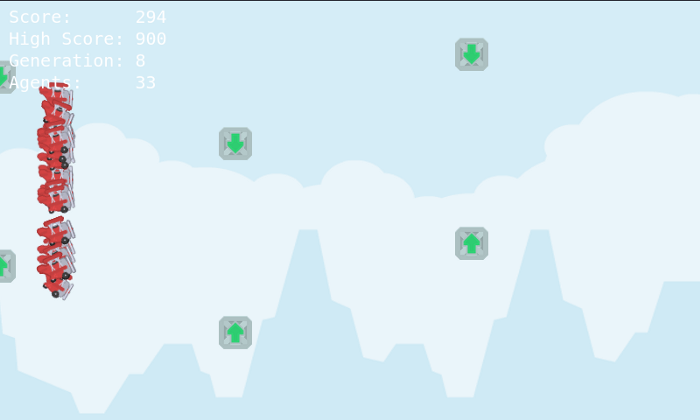
もし私が作ったとても簡易な進化的AIデモを試してみたければ、The Flappy Plane demoを開いてみてください。
お分かりいただけたように、結局いつもある時点で進化が進まなくなりニューラルネットワークはより完璧な状態へと進むことができなくなるのです。
バックプロバケーション無しでは、単純なランダム化だけではニューラルネットワークを改善することはできません。
まあ可能なのかもしれませんが、それには無限の時間が必要なので完成するまでには人類は消えているでしょう。
その突然変異はフィットネス・タイムライン・チャートでかなり早く特定することができます。
なぜなら、全ての優性のエージェントが少し良くなる瞬間は「段」として見えるからです。
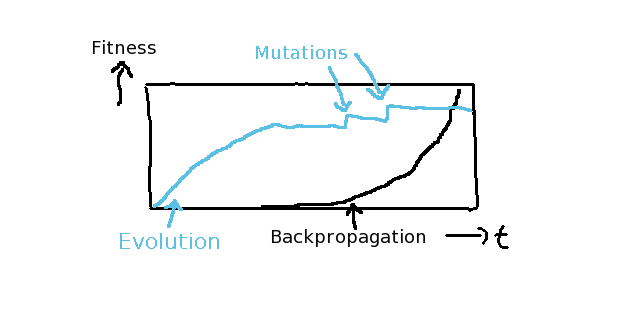
NEATやHyperNEATのような、より発展したコンセプトは、突然変異ごとのイノベーションを時間経過によって生じる、行動と突然変異の分析に基づいて解決することを目指しています。
例えば、各ゲノムの性能は独自に評価され「より良い」ゲノムだけを生存させますが、悪い方のゲノムはランダム化の改善のために記憶されます。
全ての最新の進化的コンセプトの背景にある基本的な概念は未だにランダム化を最適化させ、「既に失敗するとわかっている」ランダム値を避けることにとどまっています。
NEAT(Neuro Evolution of Augmenting Topologies)
NEATは簡単な方法で適切に説明することが困難なものです。
マリオのデモ by SethBlingを見たことがあるならこのコンセプトについて既に知っているかもしれませんね。
次に私が説明することを理解しやすくするために、この動画を見ることをお勧めします。
まず基本的なこととして、NEATはニューラルネットワークのパフォーマンスを観察して、その行動を分析するアルゴリズムであるということを覚えておいてください。
行動分析によってニューラルネットワークが向上したと判断されれば、その遺伝子は繁殖に使用されます。
逆にニューラルネットワークの向上が見られなければ、遺伝子(それともゲノム)が一時的に機能を停止させられます。
NEATは一般的に古典的な不活性のニューラルネットワークではなくANNにおいて用いられます。
全てのものが人工的と言えるので、私はANNを「適応型ニューラルネットワーク(Adaptive Neural Network)」と名付けます。
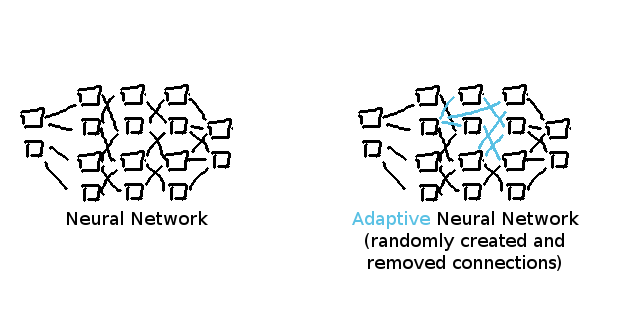
ANNというのは、ニューロンがまだないゼロの段階から始め、アルゴリズムにニューラルネットワークの完璧な構造を見つけさせるアイデアを指します。
ニューロンの接続は無作為に削除されたり構築されたりします。
その結果行動が変化することによって私たちはより効率的にニューロンを大量に発生させる場所を知ることができます。
ANNと「ドロップアウト」コンセプトやDQNコンセプトが大きく違うところは、ANNは平均的な「これなら大丈夫だと思う」というソリューションではなく、単一の完璧なソリューションを生み出すことです。
それらを用いて出来ることは大きく異なり、スーパーマリオのようなゲームでのDQNとNEATのパフォーマンスを比較してみると、ゲームのプレイ方法における大きな違いが現れます。
DQNはたぶんANNが生み出せる最高にかっこいいソリューションを生み出すことが不可能だと思います。(人類が消えるまでには無理でしょう)
NEATの持つ基本的なコンセプトは遺伝子が生産できるイノベーションを突き止めることです。
遺伝子はニューロン間の単一の繋がりを表わします。
NEATはとても整っていたので、未開の領域において様々な実装が現れました。
最もポピュラーなものはHyperNEATとES/HyperNEATです。
それらは「変わり者」であり、非常に難しいです。
今は詳細の大半は省略しますが、今後のこの記事の連載でそれらを実装してみようと思います。
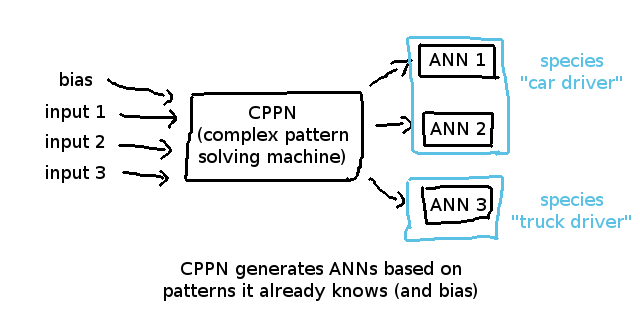
一般的なコンセプトとして、HyperNEATは行動分析の精度を上げるためにいわゆるcompositional pattern-producing network(合成パターン生成ネットワーク)または省略形のCPPNを用います。
基本的にそれはインプットの関係と測定されたニューラルネットワークの性能を学ぶ強化されたニューラルネットワークのことです。
その利点はANNの構造を記憶し、そしてその記憶とANNのエージェントの適性を関連づけられる点です。
したがって、より効率的に分類することができ、タイムライン上で「構造の変化」が「性能の変化」に与えた影響を見つけることができます。
行動分析は不要なランダム化の量を減らすというアイデアであって、結果として私たちは将来のより良い推測のためにどちらが「最も可能性の高い」値かをより良い方法で自然と推測できることです。
典型的なNEATの実装では、母集団のプールがいわゆる「エージェント」によって構成されていて、それは複数のAIが同じ問題を異なる「アイデア」で解決しようとするマルチエージェントのコンセプトに基づいているためです。
エージェントがDNAと取得したニューラルネットワークのウェイトで表される知識を生き残らせるために、常に自身が最も「最適」な存在になるよう互いに競い合うのです。
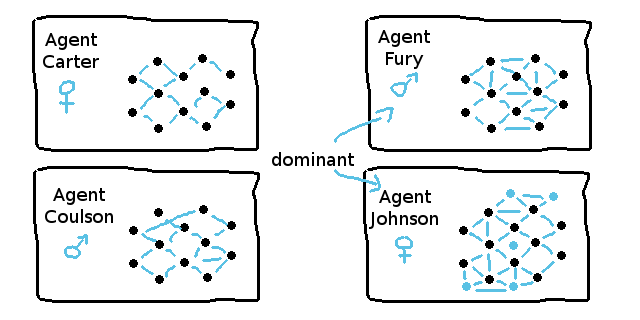
マルチエージェントシステム中の優性のエージェントは次の進化サイクルに移行するための繁殖が可能です。
次のサイクルの母集団のプールは典型的に三つの異なる種類のエージェントに分けられます。
- 20%生存者(最適なエージェントの交配繁殖)
- 20%変異体(完全にランダム化されたニューラルネットワーク)
- 60%子孫(最適なエージェントと残りの母集団の交配繁殖)
それらは基本的に健全な進化シナリオの割合で、NEATの特性でも、進化の特性でもなく、私自身の経験に基づいてできた規則です。
健全な繁殖に必要な選択肢がいつも充実しているように、健全な母集団のプールには常に少なくとも32のエージェントがあります。
小さい母集団のプールは、既知のソリューションを補強することしかできず、ランダム化に関してもより良いソリューションを生み出すチャンスを与えないため、健全な繁殖とは言えません。
進化と遺伝的プログラミングはニューラルネットワークが正しい値を見つけることに急速な発展をもたらします。
しかしながら、パフォーマンスはランダム化(とそのイノベーション)に依存している状態です。
その問題をエージェントとゲノム、遺伝子そしてニューロンの接続との関係を行動分析とフィットネス測定を用いて解決することにNEATとHyperNEATは取り組んでいます。
この連続記事の全ての内容をGitHub に作りました。
もう既にマルチエージェントシステムの基本とエージェントの適性を測る方法を知っているなら、ニューラルネットワークについて総合的により深く学ぶことができます。
典型的なAIの実装ではエージェントは脳を持っていて、そして私たちはその脳がどうなっているかを学んでいきましょう。
ニューラルネットワークに立ち返る
バックプロパゲーションの仕組み理解するため、最初にニューラルネットワーク自体に立ち返る必要があります。ニューラルネットワークは基本的にはこのようになっています:
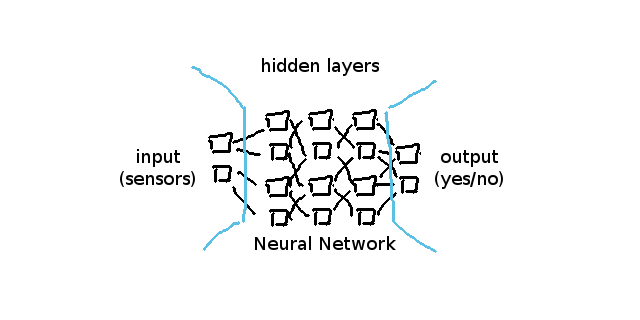
ニューロン自体が常に前の層のニューロンとのつながりを表すvalueとweightsを持っています。前と次について言及する際、前というのは、私たちのアーキテクチャチャートにおいて、より左側にある層を指します。
例えば、上記のネットワークのlayers[1]は、2 weights eachを持つ4 neuronsを持っています(layers[0]は入力層で2ニューロンを持つため)。
// A neuron inside a NN where the hidden layers
// (and input layer) have each 3 neurons
let neuron = {
value: _random(), // value for computation
weights: [ 0.5, 0.5, 0.5 ] // weights for connections
};バックプロパゲーションを理解するために、まず一歩立ち止まって、どのようにニューラルネットワークがインプリメントされているかを理解する必要があります。
怖がらないでください。単純なフィードフォワードニューラルネットワークは数行のコードで、皆さんが考えているほど複雑ではありません。
例のBrainは、後に我々のゲームと高度なNEATプロジェクトに再利用ができるように、一般的な感覚で構築されます。
ニューラルネットワークのインプリメント
Brainでは、ニューラルネットワークは、出力層、いくつかの隠れ層、出力層の3つの異なるタイプの層で構成されます。
const Brain = function() {
// TODO: Proper initialization
this.layers = [];
// input layer
// this.layers[0]
// output layer
// this.layers[this.layers.length - 1]
// each layer has multiple neurons
// this.layers[l][n] is a Neuron
};多くの人が、動作するまでにニューラルネットワークはどのくらいの大きさにするべきなのかを尋ねますが、ANNの男として、私はサイズに関して“経験則”のようなものを持っています。
それは、“最も上の入力”から“最も下の出力”への最悪のケースであるXORシチュエーションの計算を成功させるために、全ての入力ニューロンが出力ニューロンに対角線上に届かなくてはならないシュチュエーションについて考えることです。
しかしながら、もしあなたが時間的に制約のあるデータを持っているなら、これはあなたが望むものではないかもしれません。
今ここで、それを理解するのはそこまで単純ではないため、時間的制約のあるデータの問題についてはこの記事のシリーズの後半で掘り下げて行きます。
覚えておくべき重要なことは、1 inputと1 outputが最小限のシチュエーションにおいては、少なくとも私たちのネットワークには、1つの入力層、1つの隠れ層、そして1つの出力層を持つ3 layersが必要であるということです。
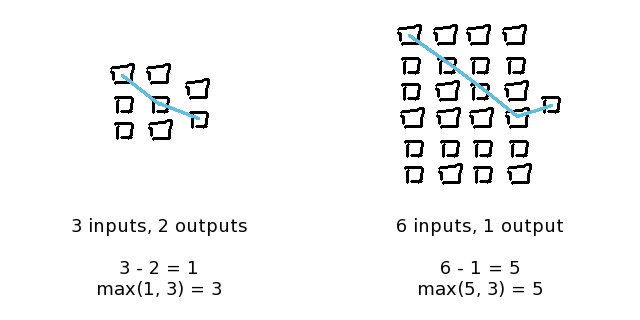
例において、斜めの線が横軸の中心を超えたところでオーバーラップしているということが重要であることに注意してください。
これにより、一番上の入力からの決定は、一番下の出力からの決定による影響を受けることになります
他の人は、それに関して様々な“強い”意見を持っており、数学的な証明を使用して、“あなたはそれに反論することができません”とかなんとか言います。
そんなことは気にしません。それは動作し、覚えやすく、そして、仕事を完了し、数学者たちが尊重しなかったシチュエーションにおいても何の問題も起こしていません。
これまで、私の経験が、私の経験則が間違っているということを証明したことは今の所ありませんが、是非、あなたはそれがうまく動作しないシナリオを見つけることに挑戦してみてください。
コードのネットワークサービスを説明するために、ニューラルネットワークを作成するための4つの異なるサイズが必要です。
- input_size は入力(センサー)の配列の長さを表す
- output_size は出力(コントロール)の配列の長さを表す
- layers_size は必要なレイヤーの量を表す
- hidden_size は隠れレイヤーあたりのニューロンの量を表す
コード内における、上記の“経験則”のインプリメンテーションはこのようなかたちです。
let input_size = 2; // or, whatever
let output_size = 2; // or, whatever
let layers_size = 3;
let hidden_size = 1;
if (input_size > output_size) {
hidden_size = input_size;
layers_size = Math.max(input_size - output_size, 3);
} else {
hidden_size = output_size;
layers_size = Math.max(output_size - input_size, 3);
}Brainのインプリメンテーション例
その経験則がどのようにコンピュータネットワークサイズに使用できるのかを分かっているので、インプリメンテーションを始めることができます。
典型的なインプリメンテーションは、JS(もしくは他言語)においてMath.random()自体が0.0から1.0の値しか生成しないため、Math.random()には-1.0から1.0でクランプできるものを入れます。
const _random = function() {
return (Math.random() * 2) - 1);
};ニューロン値とweightsはどちらも負になることがあります!なので、コードをデバッキングする時は、そのことを念頭に置いておく必要があります。
私たちはまた、最初の記事からアクティベーション機能をインプリメントする必要があることも知っています。今のところ、シグモイドは十分なので、このようにインプリメントします。
const _sigmoid = function(value) {
return (1 / (1 + Math.exp((-1 * value) / 1)));
};Brainのインプリメンテーションを続けるには、それを適切に初期化する必要があります。以前のように、ニューラルネットワークのコンテンツを表すために同じデータ構成とlayers[]配列を使用します。
ニューラルネットワークを生成する際、3種類のケース間において異なっていなければいけません。
- 入力層のニューロンは、前の層(左側)方向と繋がっていないため、weightsを持っていない
- それぞれの隠れ層のニューロンは前(左側)の層からのニューロン量と同様のサイズを持つweights[]配列を持つ
- 出力層は、隠れ層(それぞれのニューロンはweights[]配列を持つ)の行動と同一であるが、ニューロン量は出力配列のサイズです。そのため、それは隠れ層もしくは入力層と比較して異なったサイズになることもありうる。
インプリメンテーション例はこのようになります。
const Brain = function() {
this.layers = [];
};
Brain.prototype.initialize = function(inputs, outputs) {
// TODO: Task for reader - Insert Rule of Thumb from above
let input_size = 3;
let output_size = 2;
let layers_size = 3;
let hidden_size = input_size > output_size ? input_size : output_size;
this.layers = new Array(layers_size).fill(0).map((layer, l) => {
let prev = hidden_size;
let size = hidden_size;
// input layer
if (l === 0) {
prev = 0;
size = input_size;
// first hidden layer
} else if (l === 1) {
prev = input_size;
// output layer
} else if (l === layers_size - 1) {
size = output_size;
}
// neuron has value and weights (for each previous neuron)
return new Array(size).fill(0).map(_ => ({
value: _random(),
weights: new Array(prev).fill(0).map(val => _random())
}));
});
};
Brain.prototype.compute = function(inputs) {
// TODO: This will come up next
return null;
};上記のコード例が示すように、バックプロパゲーションを理解するための準備が完全にできていないため、現在、Brainを完全に無視しています。
私たちのニューラルネットワークは、現在、与えられた入力セットに対して、一見ランンダムな出力しか与えません。
あるいは、進化的または遺伝的プログラミングを使用して各ニューロンのweightを見つけることができます(前回の記事で学んだように)。
Brainのインプリメンテーションの使用法はいたってシンプルです。
// API Usage
let brain = new Brain();
let data = { inputs: [1,0], outputs: [1] };
// inititalize by reference dataset
brain.initialize(data.inputs, data.outputs);
// compute inputs and return outputs
let outputs = brain.compute(data.inputs);
console.log('computed:', outputs);
console.log('expected:', data.outputs);この使用法はすでに強化学習のために用意されているので、バックプロバゲーションを適切に理解した後、Brain.prototype.learn(inputs, outputs)のインプリメンテーションをやっと行うことができます。
上記のBrainのインプリメンテーションのフルコードはgithub repositoryで利用可能です。
フィードフォワード計算のインプリメント
フィードフォワードニューラルネットワークはニューロンのコネクション(weights)に基づいて値を転送するシンプルなNNです。
すべてのニューロンは、最初は典型的なランダムweightsを持っていることから、それらのユースケースはかなり限定されます。
しかしながら、遺伝的プログラムや進化的コンセプトを考えると、素早く、そして効率的に学習することができる効果的なNNsになることができます。
典型的なユースケースは、ブルートフォーシングや複雑なデータ構造の推測を効率的な方法で行うことです(暗号化セクターなど)。
フィードフォワードNNsはインプリメントが非常に簡単なので、バックプロパゲーション(および一般的な補強)の仕組みを理解する前に、それらについて掘り下げて行きたいと思います。
典型的なFFNNは非常にインプリメントがシンプルで、入力層(左側)から出力層(右側)への反復を行う際に、コード内において尊重しなくてはいけないユースケースはたった2種類しかありません
- 入力層は特別なケースである。Weightを持たず、それぞれのニューロン値を直接アップデートする
- それぞれの隠れ層と出力のニューロンについて、値の合計をvalues変数内にマップして保存し、それらの合計を決定します。その後、全てのニューロンに接続された値の合計であるsigmoid(value)メソッドを用いて、ニューロンを作動させます。
Brain.prototype.compute(inputs)メソッドをこのコードを用いてオーバーライドする必要があります。
Brain.prototype.compute = function(inputs) {
let layers = this.layers;
// set input values
layers[0].forEach((neuron, n) => neuron.value = inputs[n]);
// feed forward for hidden layers + output layer
layers.slice(1).forEach((layer, l) => {
let prev_layer = layers[layers.indexOf(layer) - 1];
layer.forEach(neuron => {
// neuron.weights[p] represents connection
let values = prev_layer.map((prev, p) => prev.value * neuron.weights[p])
let value = values.reduce((a, b) => a + b, 0);
neuron.value = _sigmoid(value);
});
});
// return output values
return layers[layers.length - 1].map(neuron => neuron.value);
};_sigmoid(value)メソッドは重要であり、それは前のニューロンの合計値を基準に各ニューロンを活性化します。
このneuron.value は、compute(inputs)メソッドによって返される出力配列のジェネレーション以外を再利用しないため、現在、簡単な計算目的のために存在しています。しかし、それは後に、入力値から学習するために、バックプロパゲーション用に必要になります。
各ニューロンのweight は前の層との繋がりを表します。上記のコード例はneuron.weights[p]はlayers[l — 1][p]と等しいということを意味しており、それは前の層のニューロンが同様のインデックスを持つためです。
そのため、各neuron.weights配列は、前の層(左側の層)内のニューロン量と同等のサイズです。
ニューラルネットワークは理解するために非常に重要です。経験則はアウトプットへの対角のクロスオーバーを可能にするNNレイヤー量を持つことです。フィードフォワードNNのインプリメントはとても簡単で、さらにバックプロパゲーションと強化学習テクニックに移動する前に行う必要があります。
全てのこのシリーズの記事のコンテンツと繋がっているgithub repository を作成しました。
原文
https://chatbotslife.com/machine-learning-for-dummies-part-1-dbaca076ec07
https://chatbotslife.com/machine-learning-for-dummies-part-2-270165fc1700
チャットボットライフとの提携により、翻訳し掲載しています。
チャットボットライフとは、最新のボット、AI、NLP、ツール等を扱うメディアです。
