あらすじ
ニューラルネットワークを作成する際に、層の数、ニューロンの数、活性化関数の種類等考えるべきパラメータは非常に多くあります。
そこで、これらのパラメータがどのようにモデルや学習に影響を与えるかということをscikit-learnの MLPClassifier を使って解説したいと思います。
MLPClassifierを使うと、非常に簡単にニューラルネットワークを使うことができます。
今回はそれぞれのパラメータの意味と使い方及び各種メソッドの解説していきたいと思います。
ちなみに、scikit-learnの推定器の選び方に関しては、scikit-learn(機械学習)の推定器:Estimatorの選び方 をご参照下さい。
1. hidden_layer_sizes| 層の数と、ニューロンの数を指定
default : (100,)
隠れ層の層の数と、ニューロンの数をタプルで指定します。
例えば、2層で100ニューロンずつ配置する場合は(100,100)のように指定します。
隠れ層のニューロンの数を入力層の次元(サンプルコードだと64)よりも小さくすると次元圧縮のように機能し、主成分分析のような事が可能になります。
逆に入力層の次元よりも大きくするとスパースなデータ表現を得ることが出来ます。
2. activation| 活性化関数を指定
{‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, default ‘relu’
活性化関数を指定します。
2-1. identity| 特に何もしない活性化関数
特に何もしない活性化関数です。
つまり、入力された値をそのまま出力として返し、式としては下記となります。
f(x) = x
2-2. logistic| ロジスティック関数
ロジスティック関数です。適用が簡単のため、ニューラルネットワークの活性化関数としてよく使われています。
式は
![]()
となり、グラフで書くと以下のようになだらかな曲線となります。
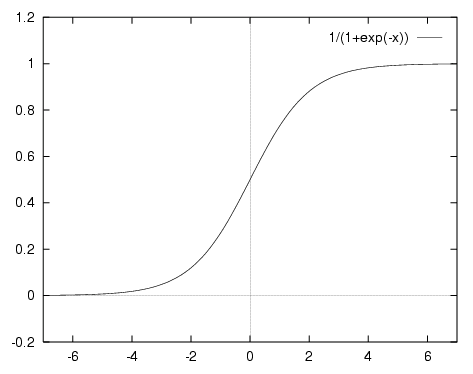
引用: https://medium.com/towards-data-science/activation-functions-and-its-types-which-is-better-a9a5310cc8f
ロジスティック関数を活性化関数として使うデメリットとしては、勾配消失問題や、学習に時間がかかることが挙げられます。
2-3. tanh| ハイパボリックタンジェントを活性化関数として使用
ハイパボリックタンジェントを活性化関数として使います。
式は以下です。
![]()
tanhは、上記のロジスティック関数で表すことが出来ます。
tanh(x)=−1+2logistic(2x)
式からもわかる通り、tanhはロジスティック関数と同じ特徴を持ちますが、tanhでは出力範囲が-1から1に変換されています。
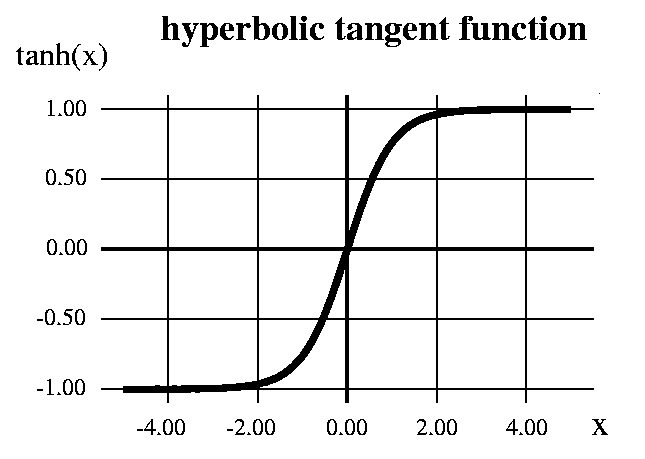
引用: https://medium.com/towards-data-science/activation-functions-and-its-types-which-is-better-a9a5310cc8f
2-4. relu| 人気でシンプルな活性化関数
Rectified Linear Unitで、ランプ関数とも呼ばれ、ここ数年で最も人気でシンプルな活性化関数です。
画像の分類等で使われる畳み込みニューラルネットワークでもほぼこの活性化関数が使われます。
微分しても常に1であるため、出力が学習の妨げになることがなく、勾配消失問題も解決出来ます。
デフォルトもreluが活性化か関数となっているので、基本はこれを使っておけば問題無いです。
式及び、グラフは下記となります。
![]()
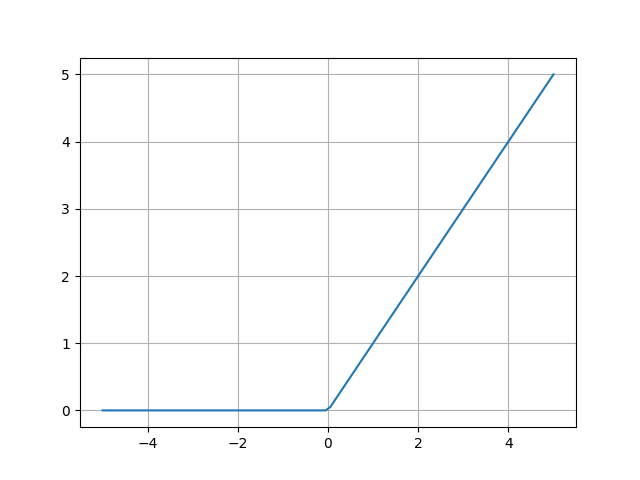
引用: http://s0sem0y.hatenablog.com/entry/2017/06/15/072248
3. solver| 最適化手法を選択
{‘lbfgs’, ‘sgd’, ‘adam’}, default ‘adam’
最適化手法を選択します。ここの選択を誤ると学習速度が遅くなったり、最終的な学習結果が最適な場所(最小値)に行き着かない可能性があります。
3-1. lbfgs
(limited memory BFGS)
準ニュートン法を省メモリにて実現した手法です。
1000以下の小さいデータセットの場合に高パフォーマンスで、高速にトレーニングが可能です。
3-2. sgd
(Stochastic Gradient Descent : 確率的勾配降下法)
初期の頃から提案されている手法です。訓練データをランダムにシャッフルし、重みを更新していきます。
この手法は確率的に局所解にはまりにくくなるという長所や、オンライン学習で使いやすいという長所を持っています。
短所としては、学習率の設定が難しい事が挙げられます。
下記の重み更新の数式のηが学習率にあたります。
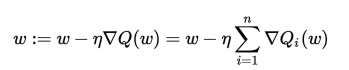
3-3. adam
(Adaptive moment estimation)
最近提案された、期待値計算に指数移動平均を使う現在最も評価されている手法です。
デフォルトもこちらの手法になっているので、基本的にこの手法を選択しておけば問題無いです。
重み更新の数式は以下。
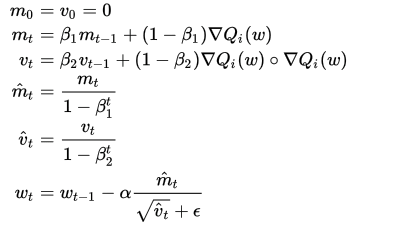
β1,β2,εの値は個別に設定が可能です。(beta_1,beta_2,epsilonのパラメータ)
過去の学習によって更新されてこなかったパラメータを優先的に更新するようなアルゴリズムになっています。
4. alpha| L2正則化のpenaltyを決定
float, optional, default 0.0001
L2正則化のpenaltyを決めます。
正則化とは、過学習を防ぐための手法で、誤差関数に付け加える重みに制約を与える項を加えます。
損失関数E(w)の代わりに下記関数を使用し、λがここで指定する値となります。
一般的に0.01 ~ 0.00001 の間の値を指定します。
![]()
この値を大きくするほど、学習時により小さい重みが重要視されるようになります。
過学習が考えられるような出力結果が得られた場合や、ネットワークの自由度が高い場合等はこのパラメータを上げてみると良いでしょう。
5. batch_size| ミニバッチのサイズ
int, optional, default ‘auto’
solverで指定した最適化手法に対するミニバッチのサイズを与えます。(lbfgsは除く)
デフォルトはbatch_size=min(200, n_samples)となります。
ミニバッチサイズを決める系統的な方法は定まっていませんが、10~100くらいを指定するか、その範囲内の出力サイズと同じとすることが多いです。
あまり大きくしすぎると最適化手法の良さが損なわれ、計算速度は落ちてしまいますので、基本はデフォルトの値で問題無いです。
6. learning_rate_init| 重みの学習率の初期値
重みの学習率の初期値を決めます。(lbfgsは除く)
大きくすると学習が早く進みますが、最適な重みに落ち着かない場合があります。
また、小さすぎると学習の進みが遅くなります。
7. learning_rate| 重みの学習率の更新方法
{‘constant’, ‘invscaling’, ‘adaptive’}, default ‘constant’
重みの学習率の更新の仕方を指定します。(solverがsgdの場合のみ有効)
7-1. constant
learning_rate_initで指定した学習率を固定で使用し、デフォルトはこちらになっています。
7-2. invscaling
一定のステップ毎にlearning_rate_initを減らしていきます。
イメージとしては、最初は大雑把に最適化していき、時間が立つ毎に細かく最適化していく手法です。
以下の式でlearning_rateが更新され、tはステップ数です。
effective_learning_rate = learning_rate_init / pow(t, power_t)
power_tはまた別のパラメータとして指定します。
使い所としては、constantで学習が非常に遅い場合、learning_rate_initを少し大きくしてこの手法を指定してみると良いかもしれません。
7-3. adaptive
学習時に、lossが減少している間はlearning_rateを固定し、2epoch連続してtol(別の指定パラメータ)の値よりもlossが減少しなかった場合にlearning_rateを1/5に減らします。
8. power_t| learning_rateの減少速度
double, optional, default 0.5
solverがsgdで、learning_rateがinvscalingの時のみ有効です。
下記の式で、どの程度の速度でlearning_rateを減少させるかを指定します。tはステップ数になります。
effective_learning_rate = learning_rate_init / pow(t, power_t)
デフォルトでは、learning_rateは√t の値で割った値になっています。
9. max_iter| 学習の反復の最大回数
int, optional, default 200
学習の反復の最大回数を定めます。
常に最大回数学習が回るというわけではなく、途中で学習が完了したと判断された場合はこれよりも早く終了します。
その判断の基準はtolのパラメータで指定します。
少なすぎると学習が進まずにいいモデルができませんが、多すぎると過学習をおこしてしまいトレーニングデータ以外のデータについてうまく判別出来なくなってしまったりします。
そのため、この値を大きくする時はearly_stoppingのパラメータをtrueにすることをおすすめします。
10. shuffle| 反復学習時のデータ・シャッフル有無
bool, optional, default True
solverがsgd,adamの時に有効で、学習を反復する毎にサンプルデータをシャッフルするかどうかを指定します。
特に意図を持って順番を固定したい場合でない限り、Trueにしておいたほうが良いモデルができます。
11. random_state| 乱数生成のためのインスタンス
int, RandomState instance or None, optional, default None
トレーニングデータをシャッフルする際などに使われる乱数生成のためのインスタンスを指定します。
デフォルトはnp.randomが使われます。
12. tol| 学習の収束値
float, optional, default 1e-4
solverがadaptiveの時以外有効
2 epoch連続してこの値よりもlossやscoreが向上しなかった場合、学習が収束したと判断され、学習を終了します。
大きくしすぎると学習途中で終了してしまいますが、小さくしすぎると過学習が起こりやすくなります。
この辺りはlossの監視やcross validation等を用いてパラメータを決めていくと良いと思います。
13. verbose| 学習の進捗状況
bool, optional, default False
Trueにすると、下記のように学習の進捗状況を出力します。
Iteration 1, loss = 5.48494375
Iteration 2, loss = 2.62731339
Iteration 3, loss = 1.41632164
Iteration 4, loss = 0.91374961
Iteration 5, loss = 0.63139715
14. warm_start| 学習済みの重み設定
bool, optional, default False
fit関数を2回め以降呼ぶ際に、既に学習済みの重みを引き継いで使うかどうかを指定し、以下のように使います。
clf = MLPClassifier(warm_start=True)
clf.fit(data_train, target_train)
clf.fit(data_train_more, target_train_more)
15. momentum| 重みの修正量
float, default 0.9
solverがsgdの場合のみ有効です。
重みの修正量に、前回の重みの修正量を加算することで、修正量が過去の修正量の重み付き平均になるので、学習の際に同じ場所を行ったり来たりすることがなくなり、SGDの収束性能をあげることが出来ます。
学習係数は0から1の範囲で定めます。
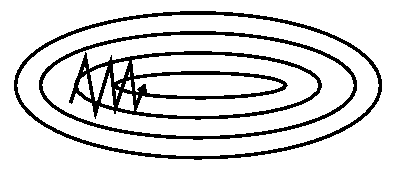
momentum無し
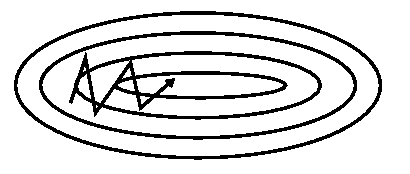
momentum有り
引用: http://ruder.io/optimizing-gradient-descent/
16. nesterovs_momentum| 重みの更新
boolean, default True
solverがsdgで、momentum>0の時に有効です。
勾配計算の段階でMomentumを考慮します。
重みの更新を以下の式で行います。
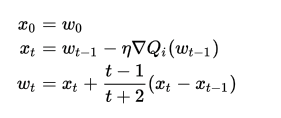
パラメータ更新を効率よく行うことが出来る様になるため、基本はTrueにしておいて問題ありません。
17. early_stopping| 学習終了値
bool, default False
solverがsgdかadamの時に有効。
Trueにすると、トレーニングデータのうちvalidation_fractionで設定されている割合(デフォルトは10%)が検証用データとして使われ、検証用データのスコアが2回連続でtolよりも低かった場合、自動的に学習を終了します。
epoch数を多く設定している場合や、トレーニングデータが十分にある場合などは使うとよいと思います。
18. validation_fraction| 検証用データの割合
float, optional, default 0.1
上記のearly_stoppingがTrueの時に、検証用データとして使うデータの割合を0~1の間で設定します。
19. beta_1| adam数式上の、β1値
float, optional, default 0.9
solverがadamの時に有効
adamの説明箇所に示した数式上の、β1の値を設定します。
論文上では初期値として0.9が推奨されています。
20. beta_2| adam数式上の、β2値
float, optional, default 0.999
solverがadamの時に有効
adamの説明箇所に示した数式上の、β2の値を設定します。
論文上では初期値として0.999が推奨されています。
21. epsilon| adam数式上の、ε値
float, optional, default 1e-8
solverがadamの時に有効で、adamの説明箇所に示した数式上の、εの値を設定します。
論文上では初期値として10^-8が推奨されています。
サンプルプログラム
以下のサンプルプログラムを使うと簡単に手書き文字判別が出来ますので、このパラメータの項を色々と変えて試してみると良いと思います。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from sklearn import datasets
from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, accuracy_score
def main():
digits = datasets.load_digits()
data = digits.data
target = digits.target
#cross_validation
data_train, data_test, target_train, target_test = train_test_split(data, target, test_size=0.2, random_state=0)
# NN learning
clf = MLPClassifier()
# lerning
clf.fit(data_train, target_train)
# preedict test data
predict = clf.predict(data_test)
# checking answer
print(classification_report(target_test, predict))
if __name__ == '__main__':
main()
