1. あらすじ
空前の人工知能ブームの昨今、ディープラーニングを始めとする、人工知能技術の中心である「機械学習」に対する期待と、世の中の需要は日に日に上昇してきています。
ディープラーニングも、ニューラルネットをベースにした機械学習の1つであり、現在の人工知能分野で主流のアルゴリズムになっていますが、それ以外にも様々な機械学習のアルゴリズムが存在し、目的によって、それらのアルゴリズムを正しく使い分ける事が重要になってきます。
今回は、その機械学習の中でも、割と古典的な学習方法である、決定木による学習方法について解説を行い、それによる、分類、及び回帰の方法の詳細について解説して参ります。
2. 機械学習の2つの手法とは?
それでは本題に入る前に、まず始めに軽く機械学習そのものに関してのおさらいをしておきます。
機械学習とは、人間が自然に行っている学習と同等の機能を、機械に学習させようという試みです。
具体的には、大量のデータを反復的に学習し、その中に潜むパターンを発見して、それに基づいて構築したモデルを用い、新たなデータの結果を予測する技術となります。
まだ結果のわからないデータを予測するという部分が、人間の知性を具体化している部分であり、それが人工知能技術の核と呼ばれる要因です。
機械学習の流れを図解すると以下のようになります。
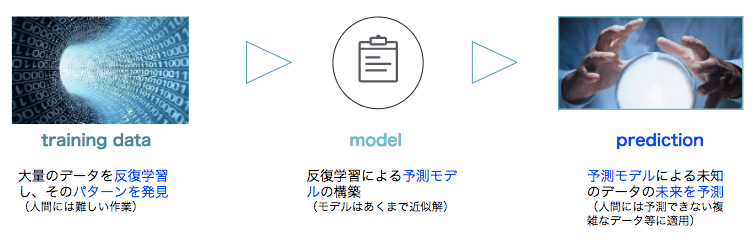
それでは、機械学習にはどのような方法があるのかについても軽くおさらいしておきましょう。
機械学習の手法を大きく2つに分けると、「分類」と「回帰」に集約されますが、
- 前者は、何らかの基準に基づいて、データを分類する事により、結果を予測する手法
- 後者は、データの、ある基準に基づいたばらつき具合(確率分布)に基づいて、結果を予測する方法
であり、基本的に機械学習は、これらのうちのどちらかをアウトプットとして行います。
この目的を達成するために、今回説明する「決定木」を使用して分類・回帰を行う方法や、「ニューラルネット」ベースで分類を実現する方法等、種々のアルゴリズムがあります。
ここでは、それぞれのアルゴリズムの詳細には踏み込みませんが、機械学習は一般的には、以下の図のような種類があります。
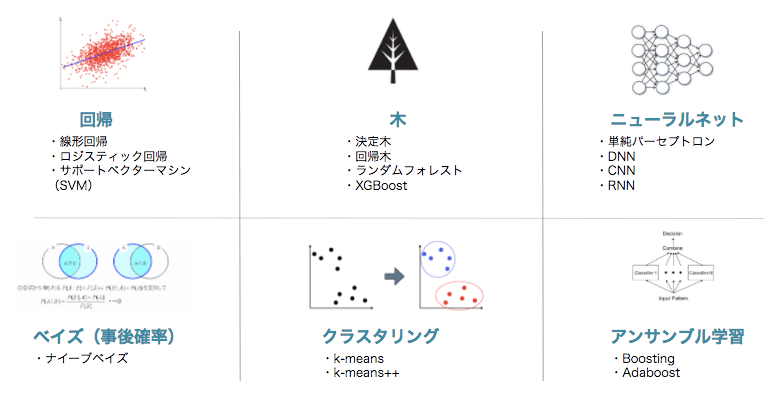
3. 決定木とは?
さて、機械学習について軽くおさらいしたので、これから本題の決定木ベースのアルゴリズムについてスポットを当てていきましょう。
決定木とは何か?それをWikipediaで確認をすると、何やら、以下のように難しい説明が書いてあります。
決定木(けっていぎ、英: decision tree)は、(リスクマネジメントなどの)決定理論の分野において、決定を行う為のグラフであり、計画を立案して目標に到達するために用いられる。
決定木は、意志決定を助けることを目的として作られる。 決定木は木構造の特別な形である。
ここから、木構造であり、何らかの意思決定を助けるために用いられるものだという事はわかりました。
それでも、よく理解できない読者の方が多いかと思いますので、以下の図をご覧下さい。
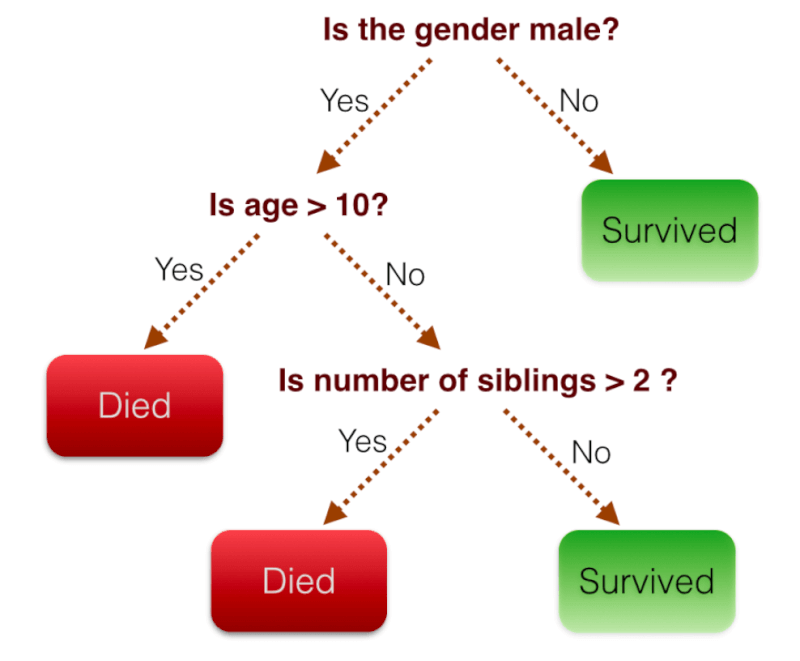
図1 (引用:http://qiita.com/yshi12/items/6d30010b353b084b3749)
上の図は、ある条件に基づいて、現在「Died」=「死んでいる」か、「Survived」=「生きている」かを決定する木構造であり、性別が男か?、年齢が10歳以上か?等の条件で、分岐をしていき、最終的に「Died」か「Survived」なのかを決定します。
最終的に「Died」か「Survived」にたどり着くまでの過程を視覚化でき、分かりやすいと言えます。
この様な因果関係がはっきりしている事象に関しては、決定木を用いて分析を行う事がよくあり、決定木はデータマイニングでよく用いられる手法となっております。
決定木を数式で表現すると、以下のようになり、yは回帰や、分類を行う対象そのものをさしており、x1 x2 x3 等は、それらを行う参考情報(上の図での条件分岐にあたるもの)を表しています。
(x, y) = (x1, x2, x3, …, xk, y)
式1
4. 決定木の種類とは?
先ほど、機械学習の種類は大別すると、「分類」と「回帰」にわけられるという話をしましたが、決定木もこれらのどちらかの目的に用いられ、それぞれ「分類木」、「回帰木」と呼ばれます。
- 分類木: 式1のyが、性別のように、分類可能な変数で、分類を目的にして、決定木のアルゴリズムを使用する場合
- 回帰木: 不動産の家賃の変動や、株価の変動等、分類ではなく、過去、及び、現在のデータから、未来の数値を予想する場合
これらが、目的に応じて機械学習で使用されます。
それでは、以下、代表的な決定木ベースの機械学習アルゴリズムである、「ランダムフォレスト」の例を解説し、その詳細を見ていきましょう。
5. ランダムフォレストの特徴とは?
機械学習を経験されている読者の方には馴染み深い名前だと思いますが、「ランダムフォレスト」という名前が示唆している通り、アルゴリズムで複数の決定木を使用して、「分類」または「回帰」をする、機械学習の代表的なアルゴリズムです。
名前の由来は、木が集まって、アンサンブル的な学習を行うので、フォレストと称されます。
以下、ランダムフォレストの特徴について解説していきます。
5-1. アンサンブル学習
ランダムフォレストという名前が示唆する通り、決定木の集合体なので、条件分岐をもった幾つかの決定木をランダムに構築して、それらの結果を組み合わせて、「分類」または「回帰」をする方法で、アンサンブル学習と呼ばれます。
いわゆる、多数決的な方法です。
また、図1で示されていた、「性別は男か?」「年齢は10歳以上か?」のような条件分岐に使われる、条件を「説明変数」と呼び、これをうまく振り分ける事が大事です。
引用:https://www.slideshare.net/HitoshiHabe/ss-58784421
5-2. バギング
アンサンブル学習を行う際の、決定木のサンプリングを行うアルゴリズムです。
通常、入力トレーニングデータからランダムサンプリングを繰り返して、無作為に決定木のサンプリングを行う事からこの名前がついています。
このように、ランダムフォレストは、比較的シンプルなアルゴリズムなので、高速に動作します。
また決定木ベースなので結果の可視化もでき、適したデータセットでは非常に精度も良くなるので、機械学習の代表的なアルゴリズムとされています。
詳しくは、【入門】アンサンブル学習の代表的な2つの手法とアルゴリズム をご参照下さい。
5-3. 決定木の深さに関して
ランダムフォレストは、ランダムにアンサンブル学習用の決定木を選び出す手法である事は説明しましたが、それでは、それらの決定木はどのように構成するといいのでしょうか?
決定木自身は、先ほど解説したバギングのアルゴリズムによって選出され、なるべく、各決定木間の相関を小さくして、分散を小さくするように選定されます。
このように選び出された決定木の分類、または、回帰の精度に起因する重要な要素は木の深さです。
一般的に、木の深さが深くなればなるほど、学習データによく適合したモデルが生成されるようになり、木の深さが浅いと、各種計算を行う際の説明変数に対する学習係数のバイアスは大きくなり、よりランダムな学習要素が盛り込まれるようになります。
経験則から、木の深さをnとすると一般的に
- 「分類」の場合は、n=1
- 「回帰」の場合は、n=5
にすると良い結果が出るとされています。
5-4. 説明変数の抽出
先ほど、図1のような決定木で、分岐に用いられている「性別は男か?」「年齢は10歳以上か?」のような条件分岐を、説明変数と呼ぶという事を説明しましたが、アンサンブル学習を行う際に、選び出す説明変数の数を決定する事も重要になります。
経験則から、説明変数の総数をpとすると一般的に
- 「分類」の場合は、√p
- 「回帰」の場合は、p/3
にすると良い結果が出るとされています。
6. ランダムフォレストの分類・回帰【詳細】
それでは、ランダムフォレストで実際に分類、回帰を行う際の詳細について見ていきます。
6-1. 分類での目的関数
まず、既に何度もお伝えしてきた通り、ランダムフォレストの肝は、アンサンブル学習を行うための各決定木の選別であり、これをうまく分割し、なるべく木間の相関を小さくして分散を小さくする事です。
これを実現するために、目的関数を使います。
![]()
式2
数式は嫌だな、、、という読者の方も多いと思いますが、数式自体を理解するよりも、その数式のもつ意味を理解する様に心がけると良いです。
- Dpは親データセットを意味し
- fは特徴量、すなわち説明変数の数
- Dleftは、親ノードから見たときの、左の子ノード
- Drightは、親ノードから見たときの、右の子ノード
- Iは不純度で、ノード中のサンプルの中に含まれている、異なった分類クラスに属しているデータの割合
をそれぞれ示しています。
つまり、式2は、なるべく不純殿偏りを、左右のノードで均等にさせようというように、分割をさせようと振舞います。
6-2. 分類での分割条件
よく使用される、分割条件は以下の3つがあります。
- エントロピー
- ジニ不純度
- 分類誤差
それぞれ詳しく内容を見ていきます。
6-2-1. エントロピー
エントロピーという言葉は、理系の学生であれば、熱力学などで登場するため、一度は耳にした事があるかと思いますが、それが情報学で使用される場合は、情報のちらばり具合を表しています。
そのちらばり具合が小さい程、エントロピーは小さくなり、また、それが大きい程、エントロピーは大きくなります。
例えば、「車」、「携帯」、「ロボット」と、3つのクラスにデータを分類したい際に、サンプルデータの中に、「車」のデータのみが含まれている場合は、エントロピーは0となります。
逆に「車」、「携帯」、「ロボット」の3つのデータが、均等にサンプルデータに含まれている場合は、エントロピーが最大になります。
![]()
式3
式3はエントロピーの計算を数式化したものです。
また、そんなものなのか、という程度に眺めて頂ければ良いですが、計算している事は、サンプル全体から、あるターゲットのクラスに属する確率を計算して、その確率と、対数をとった確率を掛け合わせたものを全クラスに対して足し合わせているといった感じです。
6-2-2. ジニ不純度
基本的にエントロピーと同じ概念で、ノードに含まれるサンプルが全て同じ場合に、最も低くなり、また、ノードに含まれるサンプルが均等にちらばっている場合に最も高くなります。
![]()
式4
式4はジニ不純殿計算式で、エントロピーの計算式の式3よりも、直感的でわかりやすいかと思います。
6-2-3. 分類誤差
ノードに含まれるサンプルの、ある特定のクラスに分類される確率を計算して、それを全体の確率から引いて、誤差を計算をします。
シンプルな方法ですが、ノードのクラスの確率の変化にはあまり敏感に反応できないため、決定木を成長させるには向きません。
![]()
式5
それでは、次に回帰の場合を見ていきましょう
6-3. 回帰での目的関数
目的関数は、分類の場合と同じく、式2となります。分類と回帰の違いは、分割方法によって変わってきます。
6-4. 回帰での分割条件
回帰の場合では、主に平均二乗誤差(MSE Mean Squard Error)が用いられ、分類と違って、多クラスを分類する訳でなく、データの散らばりの特性を見ていくため、非常にシンプルに、各ノードでの平均値からの二乗誤差を見ていく事となります。
![]()
式6
以上、ランダムフォレストを用いた、分類と回帰の方法の理論的なお話をしてきました。
ちなみに、これらのランダムフォレストの実装は、pythonの機械学習ライブラリである、scikit-learnで非常に手軽に試す事ができます。
- 分類の場合は、RandomForestClassifierクラス
- 回帰の場合は、RandomForestRegressorクラス
をそれぞれ使用します。こちらを用いたデータ分析に関しては、別記事でお話できればと思います。
