1.あらすじ
人工知能ブームの昨今、人間の話し言葉や、書き言葉を機械に学習させ理解させたり、人間の思考的なものを人工知能技術を使用して実現させようという、NLP(自然言語処理)は未来を切り開く技術として大きな注目を集めており、人工知能の花形ということができるでしょう。
NLPの応用範囲は幅広く、近年、市場を賑わせているチャットボット等のような、対話システムに用いられたり、自動文章の生成や、文章理解、文章要約等、その意味を理解するという切り口で、日常の様々な場面で応用されているテクニックです。
今回は、その中でNLPを利用した技術の1つであるトピック分析について解説をします。
トピック分析は、文章理解などを行う際に、その背後にあるトピックに関して把握をする事は非常に大事になるため、昔から多くの研究がなされている分野です。
以下、トピック解析手法の詳細について、解説をしていきます。
2.トピックモデルとは?
それでは、まず最初にトピックモデルとは何かについて解説をしていきます。
トピックという言葉をWeblioで検索すると、
言語学における話題(わだい:Topic)は、主題(しゅだい、ドイツ語: Thema、英語: theme)、題目(だいもく)などともいい、文によって陳述される中心的対象をいう。
文中に明示された場合には話題語(主題語)ともいう。
日本語では話題が前の文と同じである場合には省略することが多い(主題役割というときの「主題」とは直接関係はない)。
という記述があります。
つまり、端的にトピックを表現すると、今、話をしている話題の中の主題であり、その話の抽象度を最もあげた時の概念的なものという事ができます。
少しこの説明ではわかりにくいですが、あなたがもし、あなたの上司と仕事の件で話をしていれば、トピックは「仕事」という事になりますし、同僚と、人工知能の技術の話をしていれば、トピックは「人工知能」という事になります。
勿論、トピックは常に流動的で、トピックの解釈は、例え同じ話題について話をしていても、人によって変わってきます。
それでは、本題のトピック分析で使用される、トピックモデルとは何かというと、端的に説明をすると、文章からそれが何かを説明するためのモデルです。
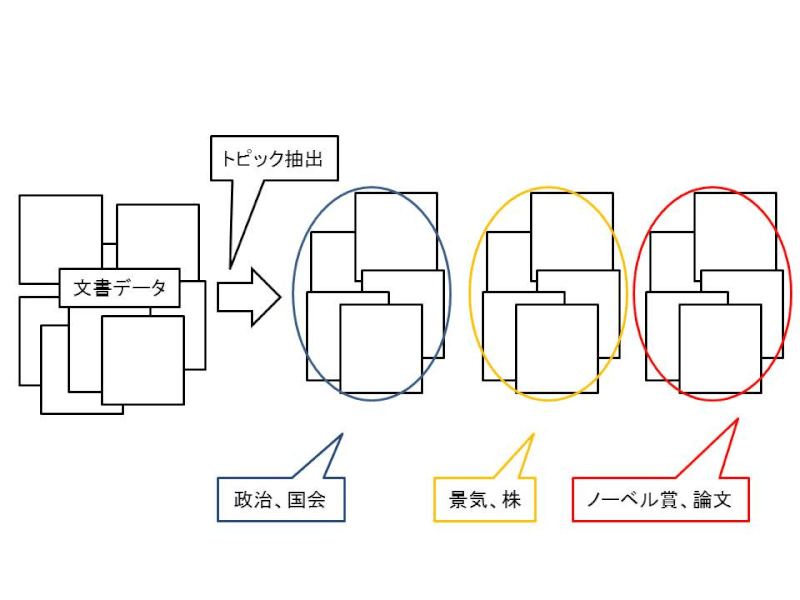
引用:http://qiita.com/GushiSnow/items/8156d440540b0a11dfe6
上の図の例のように、文章データ群があった際に、これは「政治、国会」についての話だなとか、「ノーベル賞、論文」についての話だな、各文章の主題(トピック)を判断するために、トピックモデルを構築します。
トピックモデルの適用範囲は幅広く、文章だけでなく、画像や音楽等にも適用され、単に研究のレベルではなく、実際に実運用に応用されている例もあります。
3.トピック分析の3つの手法
それでは、以下に代表的なトピック分析の手法について紹介して参ります。
トピック分析の詳細に踏み込むと、行列の次元圧縮の話など、線形代数の深い知識が必要になってくるので、少し解説が難解になってしまいますが、数式そのものの紹介より、なるべくその数式の持つ意味と、それがどのようにトピック分析に役に立つのかという部分に関してスポットを当てて話を進めていきたいと思います。
3-1.Latent Semantic Index
それでは、まずは、LSI (Latent Semantic Index)いついて紹介します。
LSIは、日本語では潜在的意味解析と呼ばれ、非常に端的にこの技術をまとめると、「自動車」「車」等、同じ意味をもつ単語をうまくグルーピングして、文章中の情報量を凝縮して、要点を強めようという圧縮技術です。
まず、LSIを使用するためには、各文章の単語が文章matrix(文章行列)として表現されている必要があります。
以下は、wheel automobile car cat dog rabbit という単語を一部含む文章を文章ベクトルに変換したイメージです。
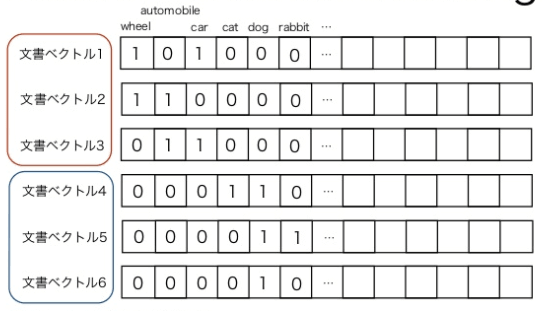
引用:https://www.slideshare.net/kogecoo/ss-47464673
文章を文章ベクトルに変換する際には、上の図のように、該当の単語が文章中にある場合は、ビットとして1を立て、それ以外は0のベクトルを生成するイメージです。
なお、文章から単語を分割する場合は、形態素解析器等を使用します。
こういった文章ベクトルがまとまったものを、文章行列と定義をします。
ここで文章ベクトルを生成していくと、全文章中に存在する単語を全て網羅しなければならなく、場合によっては文章ベクトルの次元数が、5万にも、10万にも増大し、文章ベクトルが非常に巨大になってしまい、その後の計算処理等に大きな影響を及ぼします。
そこで、この文章ベクトルを、意味の近いもの同士をまとめて、ベクトルの次元数を圧縮しようという発想がLSIとなります。この場合、carとautomobileはまとめられそうです。
さて、この文章行列の圧縮作業の詳細について解説を進めて参りますが、冒頭に述べた通り、少々、線形代数の行列関連の知識を要する内容なので、数式を紹介する際は、必ず、その意味をわかりやすく解説していこうと思います。
まず、ベクトルの圧縮技術ですが、特異値分解と呼ばれ、行列分解の手法の1つで、信号処理の分野や、統計学等に主に用いられる手法です。
特異値分解では、行と列の形の揃っている正方行列だけでなく、全ての種類の行列を分解できます。
なるべく概念をわかりやすく説明すると言いましたが、いきなり数式から入ります。
ただ、なるべくわかりやすい言葉で解説をするのでご安心を。
特異値分解を数式で表現すると以下のような式となります。
![]()
式1
Mをm行n列の任意の行列とし、行列の階級はrとします。
行列の階級というのは少し聞きなれない言葉かもしれないですが、ランク等とも呼ばれ、行列の形状に応じて、様々な階級が定義されています(詳しくはこちらを参照)。
さて、式1の意味を具体的に眺めていくと、何やら記号がでてきていますが、Mという元々の行列を、3つの成分に分解している感じです。
それぞれ、少し難しい言葉で表現すると、以下となります。
- Uは、m行r列の列直行行列
- Vは、n行r列の列直行行列
- Σは、対角要素に特異値αを降順に並べた、r行r列の対角行列
正直、理数系の学生でもなければ、この説明は全く要点を得ないかと思います。
ですので、イメージをお伝えすると、Uは文章ベクトルの基底となっており、また、Vが単語ベクトル空間の基底となっております。
ここで、実現したいことは、例えば、先ほどの「car」と「automobile」という例であれば、それらを「vehicle」という、潜在的な軸でまとめる事をしたい訳です。
また、この潜在軸がトピックの事となります。
さて、それを達成するため式1をもう少し展開します。
![]()
式2
Wは重み行列と呼ばれ、ΣとVの各成分をそれぞれ掛けわせたものとなります。
さて、Wを文章ベクトル成分毎に展開していくと以下のように表現されます。
![]()
先ほど、式1で、Σは特異値αを降順に並べた行列である、という話をしましたが、次元削減の作業とはまさに、この特異値αの小さい値を削除していくという作業になります。
基本的に、特異値αが高ければ高い程、重要度が高くなるので、αが低い、重要でない軸を探し出して、削除するのがLSIで使われる削減方法です。
正確に言うと、LSIによる次元削減方法は2種類あって、1つは行列のランクを削減するものと、もう1つは文章ベクトルの次元数そのものを削減する方法です。
ただし、これらの本質的な考え方は、今までに説明した通りです。
最後に、LSIによる次元圧縮の意味を簡単に説明すると、元の文章ベクトルのままでは、単語数が多すぎて似た内容の文章であっても、異なった文章ベクトルとして生成されてしまうこともありますが、ここで重要度の低い情報を削る事によって、この差を吸収する事にあるかと思います。
ですので、類似文章検索等によく用いられる手法です。
3-2.Probabilistic Latent Semantic Indexing
Probabilistic Latent Semantic Indexing(PLSI)は、その名の通り、LSIを確率生成モデルとして考え直したものです。
まず、いきなりですが、PLSIを数式で表現すると以下のようになります。
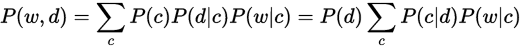
この式の意味を解説していきますが、あるドキュメントdがあって、その中の単語wに注目しています。
それを表しているのが左辺となります。
右辺の式ですが、P(d)は、ドキュメントdの出現しやすさを表しており、cは、そのドキュメント中のトピックを表しています。
つまり、P(d|c)は、この文章のトピックがcである確率を示し、P(w|c)は、このドキュメント中に出現する単語wの、トピックcにおける出現のしやすさを表しております。
また、一番右辺の式は、真ん中の式と異なるのは、トピックがcである時のドキュメントの確率を示しており、これらは対称性があります。
つまり、PLSIに最も影響を与えるパラメータは、cd + wcとなり、これらのパラメータを推定する事がキーになります。
このパラメータ推定は、EMアルゴリズムという方法で推定する事ができます。
EMアルゴリズムは、日本語では、期待値最大法と呼ばれ、詳細には踏み込んで解説は行いませんが、E(Expectation)ステップで、期待値を最大化し、M(Maximumzation)ステップで、その期待値を最大化するようなパラメータ選定を行う方法です。
PLSIの特徴としては、文章毎に複数のトピックをもつ可能性があり、また、そのトピック数の数は事前に与える必要があります。
つまり、トピック推定としてPLSIを使用するためには、その文章中のトピックの数が明確になっている必要があります。
また、トピック毎に、異なる単語の生成分布を持ち得ます。
PLSIの制約としては、取り扱える文章dは、学習時のトレーニングコーパスのものであり、新規の文章を自然に扱う事ができないという部分と、パラメータの調整が、よく過学習になりやすくなってしまう点です。
PLSIの応用先としては、情報検索分野や、NLP全般に幅広く適用できます。
3-3.Latent Dirichlet Allocation
トピックモデルとしては、LSIと並んで、このLDAも非常に有名な手法ですが、LDAは文章中の潜在的なトピックを推定し、文章分類や、文章ベクトルの次元削減等に用いられる技術です。
ここまで読んでいると、LDAの目的は、LSIとほぼ同義ですが、LDAとは何かを簡単に説明すると、PLSIをベイズ化したものです。
ベイズの定理とは、確率・統計の分野では非常に有名で、Aという事象が起こっている際に、Bの事象が起こる確率等、ある一定の条件下での確率である、条件確率について適用できる定理で、以下の式のような単純な形で表されます。
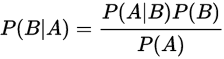
ここでは、Aという事象が起こった後に、Bという事象の条件確率は、Bという事象が起こった後に、Aという事象が起こる条件確率に、Bという事象の発生確率を掛け合わせたものを、Aという事象の発生確率で割ったものになります。
非常に有名な公式ですし、式を眺めて頂ければ、意味が直感的に理解できるかと思います。
また、このベイズの公式を使用して、観測された事象から、何らかの事項を推定する事を、ベイズ推定と呼びます。
上記のベイズ化とは、このベイズ推定の事を指しています。
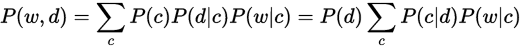
さて、こちらは先ほどのPLSIの式ですが、この式をベイズ推定する事がLDAの核となります。
上記の式は文章dまたは、トピックcの確率分布を表していますが、これを生成するための確率分布をベイズ推定により考えます。
そうすると何が嬉しいかというと、文章dに直接依存しない、トピックの確率分布を推定する事ができ、PLSIでの弱点であった、学習データにない、新規の文章も扱う事ができるようになります。
ベイズ推定に関しては、ここでは詳しく記述はしないので、Wiki 等をご参照下さい。
さて、トピックcの確率分布を推定する方法の詳細ですが、前述の通り、LDAではトピック推定の際に、文章に依存しないため、上記の式の、dは完全に忘れ去って、かわりに、dで使用される単語集合(w = w1, w2… wN)で文章を代表させます。
さて、前述の確率分布の推定ですが、トピック毎の単語の分布、文章毎のトピックの分布は、確率分布の1つの、ディレクトリ分布に従うものと仮定し、以下のように定義します。
![]()
上記は、各トピック毎に単語分布を生成しています。
![]()
上記は、各文章毎にトピックの分布を生成しています。
![]()
こちらは単語のトピックを生成しています。
さて、これらの確率分布を用いて、上記単語のトピックに該当する単語分布を選び、単語を生成する事がLDAの仕事です。
![]()
手法としては、PLSIの拡張とも言え、わかりやすいかと思います。
4.おわりに
さて、今回はこのようにトピック推定を行う際の、LSI、PLSI、LDAという3つの技術を紹介しましたが、その根底はどれも次元圧縮という観点では同じになります。
現在、これらを応用した様々なアルゴリズムが発案され、また、ライブラリ等からもお手軽に試す事が可能なため、ぜひ、これを気にお試しされてみると宜しいかと思います。
