※サンプル・コード掲載
あらすじ
GoogleのTensorFlowは機械学習計算のフレームワークであり、そのような新しいフレームワークを理解するために簡単な例から学ぶことが時に役に立ちます。
TensorFlow™ はデータフローグラフを用いた数値計算のオープンソース・ソフトウェアライブラリです。
グラフ内のノードは数学的演算を表し、エッジはノード間で伝達された多次元的データ配列を表しています。
機械学習コードで起きていることは数学であり、それは計算フローを単純化し維持することに役立ちます。
テンソルとは?
“テンソル”とはなんでしょうか? また”フロー“とどのような関わりを持つのでしょうか?
“ベクター”は値のリストであり、“マトリックス”はテーブル(もしくはリストのリスト)、そして次にテーブルのリスト(リストのリストのリスト)、さらに次にはテーブルのテーブル(テーブルのリストのリスト)があるように、これらは全て“テンソル”です。
そして、それらは機械学習の方程式ではどこにでも現れます。
例として、私たちが既に調査した一例(下記参照)を見てみましょう.
 【入門】ニューラルネットワークの仕組み
【入門】ニューラルネットワークの仕組みこの例において、入力データ(‘x1’, ‘x2’, …)は2つの層を通り、それぞれノード(‘ニューロン’)、ウェイト(‘W’)そしてバイアス(‘b’)を持ちます。
また出力はyです。
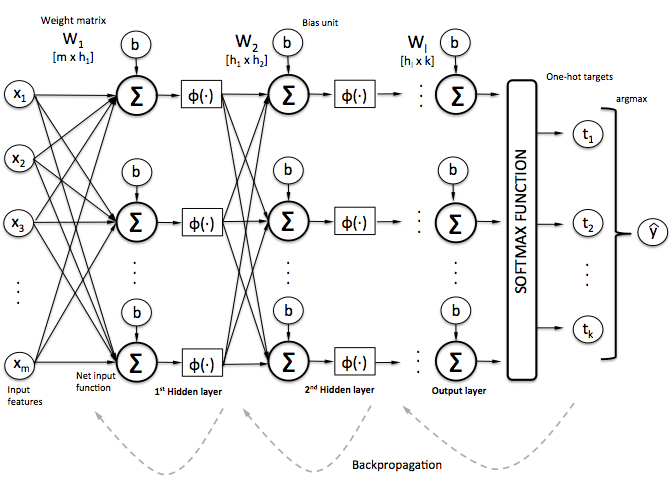
これは、入力(‘X’)から出力(‘y’)への数値計算の‘フロー’になります。
この数学には多次元的マトリクス(‘テンソル’)、定数、変数(例:バイアス‘b’)が含まれます。
テンソルを超える、この数学的フローの定義と実行がTensorflowフレームワークの概要です。
この‘フロー’を繰り返すことによって、ウェイトとバイアスが期待された出力にフィットし、モデルが構築されます。
このフレームワークはより高速な‘GPU’プロセッサーで数学的処理が可能であり、これは多くのデータを扱う際には非常に便利です。
これ以外にも、一連の方程式で多くの数学的処理を行うためのフレームワークはコードを整理し単純化させるのにも役立ちます。
TensorFlow(もしくは他の機械学習フレームワーク)のほとんどのチュートリアルは、手書き数字認識(recognizing hand-written digits)もしくは、花の分類(classifying iris flowers)に行きます。
もちろん、実践的なデータを持つことは役に立ちますが、これは機械学習初心者からすれば本当の意味での‘おもちゃ’のデータではありません。
トレーニングデータは、データ自体が直感的に掴みやすくなくてはいけません。
サンプルデータ
5ビットの配列を想像してみましょう、これが私たちの入力です。最初と最後のビットが両方ONになっているかどうかに応じて、出力は [0,1] もしくは [1,0] になります。
[0, 1, 1, 1, 1], [0,1]
[1, 1, 1, 1, 0], [0,1]
[1, 1, 1, 0, 0], [0,1]
[1, 1, 0, 0, 0], [0,1]
[1, 0, 0, 0, 1], [1,0]
[1, 1, 0, 0, 1], [1,0]
[1, 1, 1, 0, 1], [1,0]
[1, 0, 0, 1, 1], [1,0]全体のデータセットとその出力は直感的に理解することができます。
あなた(もしくは合理的感覚を持つ人であれば)は、そのデータを見るだけで直感的にパターンを見つけ出すことができるはずです。
それらのいくつかのパターンにおいて機械学習モデルをトレーニングし、その後トレーニングをしていない5ビットパターンの予測を行ったらどうなるでしょうか。
それは正しい結果の予測を行うことができるでしょうか。
これは良い‘おもちゃ’の問題であり、ソフトウェアがパターンを学習するという定義において‘機械学習’といえます。
コード
いくつかのシンプルなデータを定義し、TensorFlowでモデルを構築して、予測を行います。
そのコードがこちらで、Python notebookを使用しました。
いつものように、インポートから始めます。
import numpy as np
import random
import tensorflow as tf次にデータを作成します。
def create_feature_sets_and_labels(test_size = 0.3):
# known patterns (5 features) output of [1] of positions [0,4]==1
features = []
features.append([[0, 0, 0, 0, 0], [0,1]])
features.append([[0, 0, 0, 0, 1], [0,1]])
features.append([[0, 0, 0, 1, 1], [0,1]])
features.append([[0, 0, 1, 1, 1], [0,1]])
features.append([[0, 1, 1, 1, 1], [0,1]])
features.append([[1, 1, 1, 1, 0], [0,1]])
features.append([[1, 1, 1, 0, 0], [0,1]])
features.append([[1, 1, 0, 0, 0], [0,1]])
features.append([[1, 0, 0, 0, 0], [0,1]])
features.append([[1, 0, 0, 1, 0], [0,1]])
features.append([[1, 0, 1, 1, 0], [0,1]])
features.append([[1, 1, 0, 1, 0], [0,1]])
features.append([[0, 1, 0, 1, 1], [0,1]])
features.append([[0, 0, 1, 0, 1], [0,1]])
features.append([[1, 0, 1, 1, 1], [1,0]])
features.append([[1, 1, 0, 1, 1], [1,0]])
features.append([[1, 0, 1, 0, 1], [1,0]])
features.append([[1, 0, 0, 0, 1], [1,0]])
features.append([[1, 1, 0, 0, 1], [1,0]])
features.append([[1, 1, 1, 0, 1], [1,0]])
features.append([[1, 1, 1, 1, 1], [1,0]])
features.append([[1, 0, 0, 1, 1], [1,0]])
# shuffle out features and turn into np.array
random.shuffle(features)
features = np.array(features)
# split a portion of the features into tests
testing_size = int(test_size*len(features))
# create train and test lists
train_x = list(features[:,0][:-testing_size])
train_y = list(features[:,1][:-testing_size])
test_x = list(features[:,0][-testing_size:])
test_y = list(features[:,1][-testing_size:])
return train_x, train_y, test_x, test_y注意すべきなのは、上記の設定においてデータをシャッフルし、全体の2/3をトレーニングに使用、1/3をテストに使用しました。
その比率は‘テストサイズ’パラメータです。
実行するごとにトレーニングとテストデータのセットは異なります。
それを用いて実験を行い、結果のデータリストを確認します。
これで、私たちのTensorFlowモデルの基礎が整います。
train_x, train_y, test_x, test_y = create_feature_sets_and_labels()
# hidden layers and their nodes
n_nodes_hl1 = 20
n_nodes_hl2 = 20
# classes in our output
n_classes = 2
# iterations and batch-size to build out model
hm_epochs = 1000
batch_size = 4
x = tf.placeholder('float')
y = tf.placeholder('float')
# random weights and bias for our layers
hidden_1_layer = {'f_fum':n_nodes_hl1,
'weight':tf.Variable(tf.random_normal([len(train_x[0]), n_nodes_hl1])),
'bias':tf.Variable(tf.random_normal([n_nodes_hl1]))}
hidden_2_layer = {'f_fum':n_nodes_hl2,
'weight':tf.Variable(tf.random_normal([n_nodes_hl1, n_nodes_hl2])),
'bias':tf.Variable(tf.random_normal([n_nodes_hl2]))}
output_layer = {'f_fum':None,
'weight':tf.Variable(tf.random_normal([n_nodes_hl2, n_classes])),
'bias':tf.Variable(tf.random_normal([n_classes])),}データがロードされ、2つの層で20ノードを使用し、ランダム値を用いてウェイトとバイアスを初期化します。
また、出力レイヤーも定義します。
これで、モデルの数式を定義する準備が整います。
# our predictive model's definition
def neural_network_model(data):
# hidden layer 1: (data * W) + b
l1 = tf.add(tf.matmul(data,hidden_1_layer['weight']), hidden_1_layer['bias'])
l1 = tf.sigmoid(l1)
# hidden layer 2: (hidden_layer_1 * W) + b
l2 = tf.add(tf.matmul(l1,hidden_2_layer['weight']), hidden_2_layer['bias'])
l2 = tf.sigmoid(l2)
# output: (hidden_layer_2 * W) + b
output = tf.matmul(l2,output_layer['weight']) + output_layer['bias']
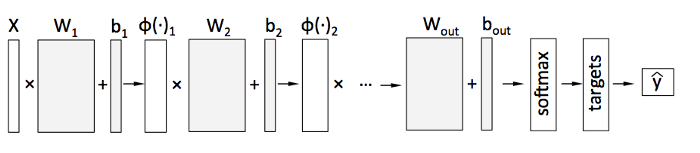
return output計算を注意深く見て、以前のダイアグラムと比較してみてください。
私たちは、(tf.matmul)データにマトリクス(‘テンソル’)、ウェイト、バイアス、そして私たちの使用しているtf.sigmoidのような関数を掛けます。
このフレームワークは機械学習で一般的に用いられているビルトイン機能を備えています。
# hidden layer 1: (data * W) + b
l1 = tf.add(tf.matmul(data,hidden_1_layer[‘weight’]), hidden_1_layer[‘bias’])l1 = tf.sigmoid(l1)それら全ては、私たちが2層のニューラルネットワークの作業(以下参照)をしていた時と同じですが、今は作業を単純化しコードを減らすフレームワークを使用しており、計算自体はぼんやりとしています。
 【入門】ニューラルネットワークの仕組み
【入門】ニューラルネットワークの仕組みそのダイアグラムと以前のコード、そしてその新しいTensorFlowコードを注意深く読んでください、それが同等のものであることがあかるはずです。
行列の乗法 はシンプルです。
そこには一切のトリックはなく、数学しかありません。
これでモデルをトレーニングする準備が整いました。
# training our model
def train_neural_network(x):
# use the model definition
prediction = neural_network_model(x)
# formula for cost (error)
cost = tf.reduce_mean( tf.nn.softmax_cross_entropy_with_logits(prediction,y) )
# optimize for cost using GradientDescent
optimizer = tf.train.GradientDescentOptimizer(1).minimize(cost)
# Tensorflow session
with tf.Session() as sess:
# initialize our variables
sess.run(tf.global_variables_initializer())
# loop through specified number of iterations
for epoch in range(hm_epochs):
epoch_loss = 0
i=0
# handle batch sized chunks of training data
while i len(train_x):
start = i
end = i+batch_size
batch_x = np.array(train_x[start:end])
batch_y = np.array(train_y[start:end])
_, c = sess.run([optimizer, cost], feed_dict={x: batch_x, y: batch_y})
epoch_loss += c
i+=batch_size
last_cost = c
# print cost updates along the way
if (epoch% (hm_epochs/5)) == 0:
print('Epoch', epoch, 'completed out of',hm_epochs,'cost:', last_cost)
# print accuracy of our model
correct = tf.equal(tf.argmax(prediction, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct, 'float'))
print('Accuracy:',accuracy.eval({x:test_x, y:test_y}))
# print predictions using our model
for i,t in enumerate(test_x):
print ('prediction for:', test_x[i])
output = prediction.eval(feed_dict = {x: [test_x[i]]})
# normalize the prediction values
print(tf.sigmoid(output[0][0]).eval(), tf.sigmoid(output[0][1]).eval())
train_neural_network(x)もう一度、どのフレームワークも使用していない2階層のニューラルネットワークの例と比較して頂ければと思います。
トレーニングの過程は同じであることがわかります。
私たちのエラー(‘コスト’)率を低くするために‘エポック’サイクルを繰り返し行います。
これでモデルの準備が整います。
出力を見た後、トレーニングコードの詳細を復習してみましょう。
Epoch 0 completed out of 1000 cost: 1.06944
Epoch 200 completed out of 1000 cost: 0.000669607
Epoch 400 completed out of 1000 cost: 0.00030982
Epoch 600 completed out of 1000 cost: 0.00019792
Epoch 800 completed out of 1000 cost: 0.00014411
Accuracy: 1.0
prediction for: [1, 1, 1, 1, 1]
0.998426 0.392255
prediction for: [1, 0, 1, 1, 1]
0.99867 0.364066
prediction for: [0, 0, 1, 1, 1]
0.028218 0.997783
prediction for: [0, 1, 0, 1, 1]
0.0528865 0.997093
prediction for: [1, 0, 0, 0, 1]
0.999507 0.413642
prediction for: [1, 0, 0, 1, 0]
0.0507428 0.9984061000サイクル以上のエラー(‘コスト’)の反復的な減少に注目してください。
その計算は、反復的にこのモデルを私たちのテストデータ(トレーニングモデルに使用したものではない)に適用した過程で処理されたものです。
その後、私たちのテストデータにおける各エントリの予測を確認することができます。
[1,0]の出力は、[1, _, _, _, 1]のパターンを意味し、[0,1] の出力はその他のパターンを意味しています。
この出力での各値は確率であるため、
prediction for: [1, 0, 0, 1, 0]
0.0507428 0.998406これは私たちのモデルが、[1, _, _, _, 1]のパターンが適用しないことを強く示唆しています。
全てのデータを今回の例のように扱うことによって、とても掴みやすく、そしてコードに集中しやすくなります。
この2階層のANNは、花の分類や株式市場トレンドに使用できるものと同じです。
トレーニングコードの詳細
トレーニングコードに話を戻します。私たちのモデルにおける変数に‘prediction’という非常にシンプルな名前を割り当てます:
# use the model definition
prediction = neural_network_model(x)次に、フレームワークにエラーを最適化する方法です。
c = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(prediction,y))
optimizer = tf.train.GradientDescentOptimizer(1).minimize(c)フレームワークに組み込まれている他のメソッドを使用することも可能です。
次に、モデルに合わせるためにループします。
with tf.Session() as sess: sess.run(tf.global_variables_initializer())
for epoch in range(hm_epochs):
_, c = sess.run([optimizer, cost], feed_dict={x: batch_x, y: batch_y})トレーニングデータの各バッチを用いて、ウェイトとバイアスの改善(エラー減少)を行います。
correct = tf.equal(tf.argmax(prediction, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct, ‘float’))
print(‘Accuracy:’,accuracy.eval({x:test_x, y:test_y}))また、いくつかの新しいデータにおける予測の作成は比較的簡単です。
0と1の出力値を正常化するため、再度、関数を使用します。
print (‘prediction for:’, test_x)
output = prediction.eval(feed_dict = {x: [test_x]})
print(tf.sigmoid(output[0][0]).eval(), tf.sigmoid(output[0][1]).eval())何が起きたのか
私たちは機械学習アルゴリズムの5ビットパターンについてお伝えし、そしてそれはトレーニングデータを見ることから学びました。
それは、パターンが何かというルールを伝えられたことによって学んだわけではなく、例を見ることによって‘学んだ’のです。
それは、些細で単純な以下のようなものでした。
def identify_pattern(data):
if data[0]==1 and data[-1]==1:
return [1,0]
else:
return [0,1]
print(test_x[0], identify_pattern(test_x[0]))もちろんこれは‘機械学習’ではなく、コードを使って問題を軽減するだけのことです。
予測モデルはnumericsの作り出すデータフローのような方程式を鍛えるのに役に立つのです。
これで、手書き数字認証(recognizing hand-written digits.)のような、リアルな問題を解決することが出来る様になりました。
原文
https://chatbotslife.com/tensorflow-demystified-80987184faf7
チャットボットライフとの提携により、翻訳し掲載しています。
チャットボットライフとは、最新のボット、AI、NLP、ツール等を扱うメディアです。
